Метод рельефов

Метод рельефов относится к групповым распределенным методам динамического управления. Критерием выбора пути в этом случае является минимальная длина пути, выраженная числом транзитных участков. Возможно использование других критери­ев, в частности времени задержки в установлении связи. Однако для определенности далее при описании метода рельефов в ка­честве критерия будет выбрано число транзитных участков.

На сети связи, где динамическое управление осуществляется методом рельефов, должны выполняться следующие операции: формирование рельефа и его коррекция. Первая из этих опера­ций выполняется в начальный момент (в момент пуска сети), а также при развитии сети, т. е. вводе в действие новых УК. Вто­рая операция осуществляется периодически в процессе функцио­нирования сети или в моменты возникновения повреждений или перегрузок на сети. Рассмотрим обе эти операции отдельно.

В момент пуска сети формирование ее рельефа начинается с некоторого узла 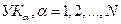, где N - число УК на се­ти, являющегося инициатором. В этом случае говорят, что начинается построение а -рельефа.

В запоминающих устройствах каждого 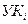сети отводится некоторый объем памяти 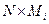(где М_i - число исходящих на­правлений из 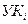), в который будет заноситься матрица релье­фов .

При формировании рельефа из УК инициатора во всех исхо­дящих из него направлениях передается цифра 1. Эта единица на соседних с УК инициатором узлах заносится в матрицу по координатам (n, т ¹), где п - номер УК инициатора, а m ¹ - но­мер ветви, по которой поступила единица.

Для примера рассмотрим сеть, изображенную на рис. 6.3, а. Пусть в каждом УК отведена область памяти для формирова­ния матрицы R (рис. 6.3, б), и пусть узлом инициатором являет­ся 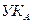. В этом случае цифра 1 будет занесена в матрицы 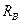и .

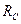Далее процесс построения рельефа протекает следующим образом. Все УК, в которые поступила цифра 1, передают по всем исходящим направлениям, за исключением того направле­ния, по которому поступила 1, цифру 2. Эта цифра во всех УК, в которые она поступила, заносится в матрицу по координа­те (n, m ²), где т² - номер ветви, по которой поступила цифра 2. Для рассматриваемого примера цифра 2 будет занесена в мат­рицы .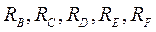

Теперь УК, на которые поступила цифра 2, передают по ис­ходящим направлениям цифру 3 и т. д. При этом должны со­блюдаться следующие правила:

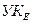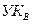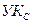1. Если в УК поступили одинаковые цифры с двух и более направлений, данный УК инициирует передачу цифры на единицу больше поступившей по всем без исключения исходящим на­правлениям. Например, в цифра 2 поступает с направлений, идущих от и . В этом случае цифра 3 с 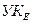передается по всем исходящим направлениям.

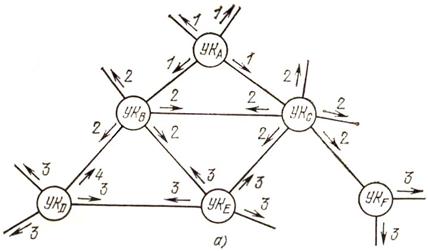
Рис. 6.3

2. Если в УК поступает минимальная цифра с одного направления, на дан­ном УК происходит инициация для передачи цифры на единицу больше той, которая поступила по всем направлениям, за ис­ключением того направления, по которому передана данная циф­ра. Передача цифры по этому направлению возможна лишь при поступлении в данный УК следующей цифры. Цифра, передавае­мая по этому направлению, должна быть на единицу больше цифры, поступившей второй по порядку. Например, в 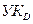циф­ра 2 поступает по одному направлению - от 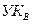. Тогда цифра 3 с 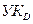должна передаваться по всем направлениям, за исклю­чением направления к 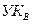. По этому направлению будет пере­дана цифра 4, так как следующая по порядку цифра, поступив­шая в 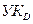это цифра 3.

3. Инициация передачи цифр по всем направлениям на каж­дом УК происходит 1 раз после поступления первой цифры по порядку. Например, при передаче цифры 3 на 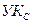с 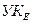она заносится в матрицу 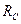по соответствующим координатам, а инициация передачи следующей по порядку цифры уже не происходит, так как ранее была осуществлена передача цифры 2.

Таким образом, для рассматриваемого примера будет сфор­мирован А -рельеф. Аналогичным образом строятся рельефы для всех остальных узлов сети. Считается, что рельеф сети сформи­рован, если построены все а -рельефы (а =1, 2,..., N).

Поиск оптимального пути установления соединения от 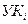, к 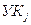состоит в отыскании в 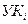и каждом промежуточном УК ветви, которой соответствует минимальное число в строке матри­цы рельефов для .

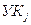Пусть требуется установить соединение от 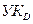к 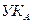(см. рис. 6.7, а). В этом случае на 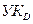происходит обращение к строке матрицы рельефов со­ответствующей 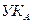(см. рис. 6.3, б). Соединение устанавливается по вет­ви, которой соответствует минималь­ное число в этой строке. Для рассмат­риваемого примера это ветвь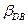. На 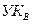процесс поиска оптимального пу­ти повторяется. В данном случае бу­дет выбрана ветвь 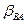. Если в этой ветви нет свободных каналов, то вы­бирается ветвь, которой соответствует следующее по порядку число, т е. ветвь , и т. д.

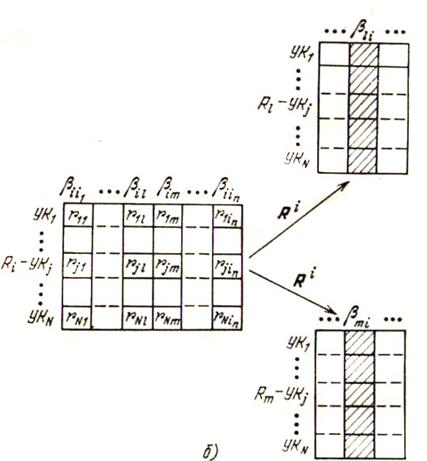
Рис. 6.4

При выборе пути установ­ления соединений на сети с об­ходными направлениями, в том числе и по методу рельефов, возможно возникновение так называемых «петель», т. е. ког­да соединение дважды прохо­дит через один и тот же узел.

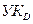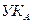Пусть требуется установить со­единение от к . На 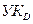вы­бирается ветвь 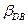. Теперь пусть в ветви 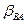нет ни одного свободного канала, тогда вызов согласно матри­це 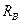перенаправляется по ветви . Если в ветви 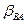тоже нет свободных каналов, то согласно матрице 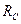вы­зов должен быть направлен обратно на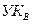. Это первый тип «петли». При соответствующей ситуации данный вызов может «блуждать» в сети по такой петле: 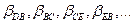Следовательно, в этом случае вызов дважды попадает в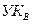. Это второй тип «петли».

Очевидно, что появление «петель» как первого, так и второго типов недопустимо. Один из способов борьбы с возникновени­ем «петель» заключается в том, что в процессе распространения по сети вызов «запоминает» номера УК, через которые он прошел, чтобы не проходить через них дважды.

Таким образом, соединения на сети должны, устанавливаться в соответствии со сформированными матрицами рельефов без образования «петель». Следует отметить, что, поскольку ситуация на сети непрерывно меняется (одни направления перегру­жаются, а нагрузка в других направлениях уменьшается; кроме того, могут выйти из строя каналы связи, возникнуть повреждения в отдельных направлениях связи и УК), появляется необходимость в коррекции рельефа сети. Рассмотрим процесс обме­на служебной информацией между управляющими устройствам (УУ) соседних узлов 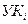, 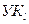и 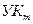(рис. 6.4, а) при коррекции рельефа сети связи.

Пусть в 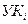хранится матрица рельефов , (см. рис. 6.4, б), и пусть поступил сигнал начала передачи служебной информа­ции о рельефах на соседние УК. Тогда УУ считает из ЗУ, в котором хранится матрица , элементы – первой строки и найдет минимальный из них.

Предположим, что минимальным элементом, т. е. элементом с минимальной высотой 1-рельефа, будет 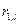. Это означает, что кратчайший путь из 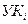, до 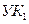проходит через узел 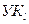, а число транзитных участков в нем равно 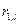. Согласно операциям форми­рования рельефа УУ, прибавив единицу к этому элементу, полу­чит элемент 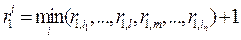, который необходимо передать на соседние узлы. Значение 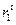, очевидно, равно высоте 1-рельефа тех ветвей, которые связывают узлы с .

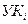Однако в рассматриваемой распределенной системе динами­ческого управления элемент 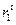не передается на соседние узлы до тех пор, пока не будут определены другие элементы, соответ­ствующие другим рельефам, т. е.

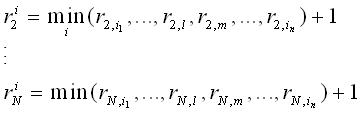
Эти элементы образуют вектор

.

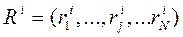После того как вектор 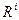полностью вычислен управляющим устройством, 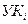передает его в УУ всех соседних УК (см. рис. 6.4, б), при этом он записывается в ЗУ этих УК в качестве столбца матрицы рельефов. Точно такие же операции выполняют управляющие устройства всех остальных УК.

Если в ветви, например, 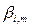отсутствуют каналы или она повреждена, то при вычислении элемента 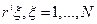,принимаем .

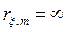Дата добавления: 2014-01-07