Формировании решений

Основные понятия теории измерений при

Основы теории принятия решений

Измерение определяется как процедура сравнения объектов по определенным показателям (признакам). В определение включены три понятия: объекты, показатели и процедура сравнения. Для формального описания множества объектов и отношений между ними при фиксированных показателях сравнения вводится понятие «эмпирические системы» с отношениями, т.е. M= á O, R ñ, где, О = 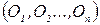– множество объектов, 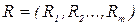- множество отношений между объектами. Запись 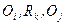означает, что объекты O_i и О_j находятся между собой в отношении R_k, такое отношение называется двухмерным (бинарным) поскольку оно связывает два объекта, если три – трехмерным.

Принято три класса отношений между объектами: эквивалентности, строгого порядка и квазипорядка.

Эквивалентность означает неразличимость объектов по принятым показателям (для обозначения принят специальный символ ~, например, если О_i и O_j, эквивалентны, то записывают в виде Оi ~ Оj).

Для обозначения отношения строгого порядка используется символ, например, если О_i предпочтительнее O_j, то записывают, O_i O_j.

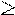
Для обозначения квазипорядка используется символ ¢. Например, если O_i ¢ O_j, это значит, что объект O_i «не хуже» O_j.

Разнообразие возможных объектов, показателей сравнения и видов отношений, встречающихся в реальных измерениях, привело к необходимости установления универсальной системы с отношениями. В качестве такой системы используется числовая система с отношениями H=< N,S >, где N - множество действительных чисел, S = (S₁,S₂…S_m)- множество отношений между числами.

Отношению эквивалентов между объектами соответствует отношение равенства между числами. Отношению порядка между объектами соответствует отношение неравенства между числами.

Числовая система используется для унификации процесса измерения. Измерение заключается в отображении объектов эмпирической системы на множество чисел таким образом, чтобы отношение между числами, отображающими объекты, сохраняли отношение между самими объектами. Для того, чтобы числовая система сохранила свойства и отношения объектов, необходимо, чтобы она была изоморфной или гомоморфной эмперической системе. Числовая система изоморфна эмпирической системе, если они подобны и между ними существует взаимно-однозначное отображение (функция f - объектов на множество чисел) такое, что отношение f_k между объектами имеет место тогда и только тогда, когда имеет место отношение S_k между числами, отображающими объекты на числовой оси. Подобие двух систем с отношениями означает, что количество отношений и их мерность в обеих системах одинаково.

Условие взаимной однозначности отображения f является в ряде случаев слишком жестким и не всегда необходимым. Если устранить это условие из предыдущего определения изоморфизма, то будем иметь дело с понятием гомоморфизма.

Основными проблемами теории измерений являются проблемы представления и единственности. Проблема представления заключается в доказательстве того, что для эмпирической системы, выбранной с целью измерения определенных свойств объектов можно построить изоморфную или гомоморфную числовую систему, описывающую свойства объектов и отношений между ними с помощью чисел.

Проблема единственности заключается в определении всех возможных способов представления заданной эмпирической системы различными числовыми системами и как связаны между собой эти числовые системы.

Проблему единственности можно сформулировать как проблему определения типа шкалы. Шкалой называется совокупность эмпирической систем, числовой системы и отображения, т.е. Ш=< М,H,f >. Пусть Ш₁=<M,H,f> и Ш₂=<М,H,g>, две шкалы, различающиеся отображениями f и g; тогда возникает вопрос о взаимосвязи числовых значений, полученных этими изображениями одного и того же объекта. Например r_i=f(O_i), z_i=g(O_i). Связь между числами r_i и r¢_i запишем с помощью функции Y: (r_i) = Y(r¢_i) или f(O_i) = Y [ g(O_i) ]. Функция Y называется допустимым преобразованием шкалы. Эта функция устанавливает связи между всеми числовыми системами, выбираемыми для описания одной и той же эмпирической системы.

Свойства функции Y определяют тип шкалы и, следовательно, позволяют произвести научно обоснованную классификацию шкал измерения.

Единственность описания эмпирической системы числовыми системами выражается в свойствах допустимого преобразования шкалы, т.е. в свойствах функции Y.

< OR >

< HS > < HS >

f (O_i) = Y [ g (O_i) ]

Рис. 8. Схема отображения объектов эмпирической системы на числовую систему

На рисунке 8 схематически показано отображение объектов эмпирической системы на числовую систему с помощью разных функций f и g. Связь между разными числами f (O_i) и g (O_i), описывающими один и тот же объект, определяется допустимым преобразованием Y.

В практике измерений наиболее часто используются шкалы следующих типов: шкала наименований, порядковая шкала, шкала интервалов, шкала отношений, шкала разностей, абсолютная шкала. Кратко остановимся на каждом типе.

Шкала наименований используется для описания принадлежности объектов к определенным классам. Всем объектам одного и того же класса присваивается одно и то же число, а объектам разных классов разные числа. В связи с этим шкала наименований часто называется шкалой классификации. Шкала используется на практике при составлении классификации. Шкала сохраняет отношения эквивалентности и различия между объектами. Широко используется на практике при составлении классификаторов АСУ и т.д. Существует большое число вариантов присвоения чисел классам эквивалентных объектов. В связи с этим понятие единственности отображения состоит для шкалы во взаимооднозначности допустимого преобразования Y. Это означает, что если имеются два варианта приписывания классам числовых значений, то они должны быть связаны между собой взаимооднозначно, что позволяет установить связь между числовыми вариантами описания классов эквивалентности. Таким образом, шкала наименований единственна с точностью до взаимооднозначного преобразования.

Шкала порядка применятся для измерения упорядочения объектов по одному или совокупности признаков (например, шкала твердости минералов). Шкала порядка широко используется при экспертном оценивании для упорядочения объектов. Для порядковой шкалы допустимое преобразование Y.

является любым монотонным преобразованием. Следовательно, шкала порядка единственна с точностью до монотонного преобразования. Числа в шкале определяют порядок следования объектов и не дают возможности сказать, на сколько или во сколько раз один объект предпочтительнее другого.

Шкала интервалов применяется для отображения величин различия между свойствами объектов. Примером использования этой шкалы является измерение температуры. При экспертном оценивании шкала интервалов применяется для оценки полезности объектов. Основным свойством шкалы интервалов является равенство интервалов. Интервальная шкала может иметь произвольные точки отсчета и масштаб. Допустим преобразованием Y для шкалы интервалов является линейное преобразование I (x) = ax+b. Следовательно, шкала интервалов единственна с точностью до линейного преобразования. В этой шкале отношение разности чисел в двух числовых системах определяется масштабом измерения.

Шкала отношений используется, например, для измерения массы, длин, веса, цены. В этой шкале числа отражают отношения свойств объектов, т.е. во сколько раз свойство одного объекта превосходят это же свойство другого объекта. Допустимым преобразованием шкалы является преобразование подобия: Y(x)=ax. Отсюда следует, что шкала отношений является частным случаем шкалы интервалов при выборе нулевой точки отсчета b = 0.

Шкала разностей используется для измерения свойств объектов при необходимости выражения на сколько один объект превосходит другой по одному или нескольким признакам. Эта шкала является частным случаем шкалы интервалов при выборе единичного масштаба. Следовательно. Допустимое преобразование для шкалы разностей есть преобразование сдвига Y(x) = x+b.

Абсолютная шкала является частным случаем шкалы интервалов. В этой шкале принимается нулевая точка отсчета и единичный масштаб. Допустимым преобразованием для абсолютной шкалы является тождественное преобразование, т.е. I(x)=X. Это значит, что существует одно отображение объектов в числовую систему. Отсюда и следует название шкалы, так как для нее единственность отображения понимается в буквальном, абсолютном смысле. Абсолютная шкала применяется, например, для измерения количества объектов (предметов, событий, решений и т.п.). Количество объектов измеряется единственным образом с помощью натуральных чисел 1,2,…….,n.

Дата добавления: 2014-01-07