
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Групповая оценка объекта
|
|
|
|
Рассмотрим алгоритм обработки результатов экспертного оценивания множества объектов. Пусть d экспертов произвели оценку m объектов по e показателям. Результаты оценки представлены в виде величины хnis, где s – номер эксперта, i – номер объекта, n – номер показателя (признака) сравнения. Если оценка объектов произведена методом ранжирования, то величины хnis представляют собой ранги. Если оценка объектов выполнена методом непосредственной оценки или хnis методом последовательного сравнения, то величины хnis представляют собой числа из некоторого отрезка числовой оси или баллы. Обработка результатов оценки существенно зависит от рассмотренных методов измерения.
Рассмотрим вариант, когда величины хnis (x = 1, 2,..., d; i = 1,..., m; h = 1,., е) получены методом непосредственной оценки или последовательного сравнения, т.е. являются числами или баллами. Для получения групповой оценки объектов в этом случае можно воспользоваться средним значением оценки для каждого объекта
 (29)
(29)
где qn коэффициенты весов показателей сравнения объектов, ks – коэффициенты компетентности экспертов. Эти коэффициенты являются нормированными величинами
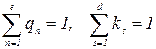 (30)
(30)
Коэффициенты весов показателей могут быть определены экспертным путем. Если qns – коэффициент веса n -го показателя, присваемый s -м экспертом, то средний коэффициент веса n -го показателя по всем экспертам равны
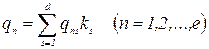 (31)
(31)
Получение групповой экспертной оценки путем суммирования индивидуальных оценок с весами компетентности и важности показателей при изменении свойств объектов в количественных шкалах основывается на предположении и выполнении аксиом теории полезности как для индивидуальных, так и групповой оценок и условий неразличимости объектов в групповом отношении, если они неразличимы; во всех индивидуальных оценках. В реальных задачах эти условия как правила выполняются, поэтому получение групповой оценки объектов путем суммирования широко применяется на практике.
Коэффициенты компетентности экспертов можно вычислить результатам оценки объектов. Основной идеей этого вычисления является предположение о том, что компетентность экспертов должна оцениваться по степени согласованности их оценок с групповой оценкой объектов.
Алгоритм вычисления коэффициентов компетентности экспертов имеет вид рекуррентной процедуры
 (32)
(32)
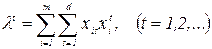 (33)
(33)
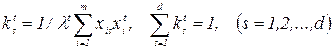 (34)
(34)
Вычисления начинаются с t = 1. В формуле (32) начальные значения коэффициентов компетентности принимаются одинаковыми и равными k0s = 1 / d. Тогда в формуле (32) групповые оценки объектов первого приближения равны средним арифметическим значениям оценок экспертов.
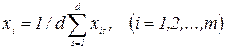 (35)
(35)
Далее вычисляется величина  по формуле (33)
по формуле (33)
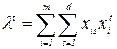 (36)
(36)
а значения коэффициентов компетентности первого приближения до формуле (34)
 (37)
(37)
Используя коэффициенты компетентности первого приближения можно повторить весь процесс вычисления по формулам (32), (33), (34) и получить вторые приближения величин хi2, l2, ks2.
Пример 2. Три эксперта (d = 3) оценили значение двух мероприятий (m = 2) по решению одной проблемы (е = 1), приведя нормирование опенки х13 + х23 = 1 мероприятий, представленные в таблице (11).
Таблица 11
| эксперты мероприятия | Э1 | Э2 | Э3 |
| М1 | 0,3 | 0,5 | 0,2 |
| М2 | 0,7 | 0,5 | 0,8 |
Проведем вычисление групповых оценок мероприятий и коэффициентов компетентности экспертов по формулам (32), (33), (34). Средние оценки объектов первого приближения по формуле (32) при t = 1 равны
х1' = 1/3 (0,3 + 0,5 + 0,2) = 0,335
х1' = 1/3 (0,7 + 0,5 + 0,8) = 0,665
Вычислим величину l' по формуле (37).
l' = 1 × 0,335 + 2 × 0,665 = 1,665
Вычисляем коэффициенты компетентности первого приближения по формуле (30):
k11 = (1 / 1,665) × (0,3 × 0,335 + 0,7 × 0,665) = 0,34
k11 = (1 / 1,665) × (0,5 × 0,335 + 0,5 × 0,665) = 0,30
k31 = (1 / 1,665) × (0,2 × 0,335 + 0,8 × 0,665) = 0,36
Вычисляя групповые оценки объектов второго приближения получаем вектор х2 = (0,324; 0,676). Величина l2 = 1,676. Вектор коэффициентов компетентности второго приближения равен k2 = (0,341; 0,291; 0,361). Для третьего приближения получаем х3 = (0,3235; 0,6765), l3 = 1,6765, k3 =(0,341; 0,298; 0,361). Как следует из результатов третьего приближения, вектор коэффициентов компетентности стабилизировался. Поэтому дальнейшие вычисления не дадут существенного уточнения.
Рассмотрим вариант, когда эксперты производят измерения объектов в порядковой шкале методом ранжирования, так что величины хisn, где i – номер объекта, s – номер эксперта, n – номер показателя сравнения объектов, есть ранги. Задачей обработки является построение обобщенной ранжировки по индивидуальным ранжировкам экспертов. Для простоты рассмотрим вначале случай одного признака сравнения, поэтому индекс n у величины хisn опустим. Каждую ранжировку, используя отношение квазипорядка и числовое представление
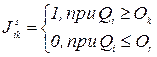 (38)
(38)
можно представить, в виде матрицы парных сравнений с булевыми переменными 0,1. Связь переменных Jiks с переменными хis выражается соотношением
 (39)
(39)
где хis и хks – ранги, присваиваемые s -м экспертом i -му и k -му объектам. Пусть, например, дана ранжировка (один эксперт, т.е. s = 1).
 O1 O2 ~ O3 O4 O5
O1 O2 ~ O3 O4 O5
Тогда матрица парных сравнений для этой ранжировки изображена в таблице (12).
Если имеется d экспертов, то каждый эксперт дает свою ранжировку, которой соответствует матрица парных сравнений. Таким образом, количество матриц парных сравнений равно числу экспертов.
Введем расстояние — метрику между матрицами парных сравнения, которое вычисляется по формуле
 , (s, l = 1, 2,..., d) (40)
, (s, l = 1, 2,..., d) (40)
Таблица 12
| O1 | O2 | O3 | O4 | O5 | |
| O1 | |||||
| O2 | |||||
| O3 | |||||
| O4 | |||||
| O5 |
Смысл этого выражения состоит в том, что расстояние между матрицами парных сравнений определяется числом поразрядных несовпадений всех значений элементов матриц.
Используя эту метрику, определим обобщенную ранжировку как такую матрицу парных сравнений, которая наилучшим образом согласуется с матрицами парных сравнений, получаемыми из ранжировок экспертов. Понятие наилучшего согласования на практике чаще всего определяют как медиану и среднюю ранжировку.
Медиана есть такая матрица парных сравнений, сумма расстоянии от которой до всех матриц парных сравнений, получаемых от экспертов, является минимальной.
 (41)
(41)
Средняя ранжировка есть такая матрица парных сравнений, сумма квадратов расстояний от потери до всех матриц парных сравнений, полученных при экспертизе является минимальной
 (42)
(42)
Покажем, что построение матрицы парных сравнений, соответствующей медианы осуществляется по принципу простого большинства голосов экспертов для каждого элемента матрицы. Модуль равности булевых переменных (41) равен либо единице, либо нулю, поэтому модуль разности равен квадрату этой разности. Следовательно, вместо выражения (41) можно записать:
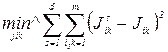 (43)
(43)
Возводя члены в круглой скобке в квадрат и учитывая, что квадрат булевой переменной равен самой переменной, получаем, что элементы обобщенной матрицы парных сравнений определяется но правилу большинства голосов, (т.е. принимается Оi > Оk если больше половины экспертов высказались за это предпочтение).
В рассмотренном алгоритме построения обобщенной матрицы парных сравнений можно учесть компетентность экспертов, путем введения коэффициентов компетентности k, в соотношении (41).
 (44)
(44)
Выполняя преобразования, получим для случая учета коэффициентов компетентности экспертов следующее правило построения обобщенной матрицы парных сравнений:
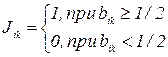
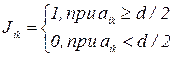 (45)
(45)
где величины bik равны
 , (i, k = 1, 2,..., m) (46)
, (i, k = 1, 2,..., m) (46)
При наличии нескольких ситуаций эксперты упорядочивают объекты (решения) для каждой ситуации в отдельности. Если известны вероятности ситуации Р1, Р2,..., Рn, где n – количества ситуаций, то можно построить обобщенною ранжировку, осредненную по всем ситуациям. Введем у элементов матриц парных сравнений индекс J – номер ситуации Jikjs. В этом случае обобщенная матрица парных сравнений будет определяться из условий
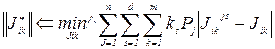 (47)
(47)
Выполняя преобразования, получаем следующее правило построения элементов обобщенной матрицы парных сравнений, осредненных с помощью вероятностей по всем ситуациям
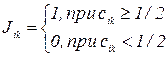 (48)
(48)
где величины cik равны
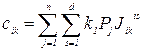 (49)
(49)
В частном случае одинаковой компетентности экспертов ks опускается.
После получения обобщенной матрицы парных сравнений необходимо построить обобщенную ранжировку. Наиболее простым способом получения ранжировки из матрицы парных сравнений является применение задачи о лидере. Используя рекуррентную процедуру вычисления относительных весов объектов, аналогичную вычислению коэффициентов экспертов
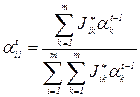 , (i = 1, 2,..., m; t = 1, 2) (50)
, (i = 1, 2,..., m; t = 1, 2) (50)
нетрудно определить упорядочение объектов. В этой формуле t – номер шага, i – номер объекта,  – коэффициент относительного веса объекта. Сумма коэффициентов относительных весов объектов на каждом шаге равна единице. Для первого шага t = 1 формула имеет вид:
– коэффициент относительного веса объекта. Сумма коэффициентов относительных весов объектов на каждом шаге равна единице. Для первого шага t = 1 формула имеет вид:
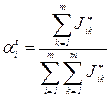 (51)
(51)
В соответствии с этой формулой коэффициенты на первом шаге определяются как сумма единиц в i -й строке обобщенной матрицы парных сравнений, поделенная на сумму всех элементов этой матрицы. По величине  производится упорядочение объектов. Чем больше
производится упорядочение объектов. Чем больше  , тем предпочтительнее i -й объект. Если по коэффициентам первого приближения получено строгое упорядочение объектов (т.е. нет эквивалентных объектов), то оно не изменится при вычислении последующих приближений.
, тем предпочтительнее i -й объект. Если по коэффициентам первого приближения получено строгое упорядочение объектов (т.е. нет эквивалентных объектов), то оно не изменится при вычислении последующих приближений.
В частном случае, когда производится ранжировка множества объектов одинаково компетентными экспертами для построения обобщенной ранжировки, можно использовать способ сумм рангов. При этом необходимо, чтобы ранги задавались в виде натуральных чисел (1,2,..., m). Для каждого объекта вычисляется сумма хsi. По этим суммам производится упорядочение объектов таким образом, что первое место получает объект с наименьшей суммой, а последнее место объект с наибольшей суммой.
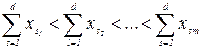 (52)
(52)
Значение суммы рангов для каждого объекта есть сумма мест, присужденных данному объекту всеми экспертами.
Пример 3. В результате проведения ранжировок четырех объектов пятью экспертами получены упорядочения объектов, представленных в таблице 8.
Таблица 13
| O1 | O2 | O3 | O4 | |
| Э1 | ||||
| Э2 | ||||
| Э3 | ||||
| Э4 | ||||
| Э5 |
Таблица 14
| O1 | O2 | O3 | O4 | |
| О1 | ||||
| О2 | ||||
| О3 | ||||
| О4 |
Таблица 15
| O1 | O2 | O3 | O4 | |
| О1 | ||||
| О2 | ||||
| О3 | ||||
| О4 |
Таблица 16
| O1 | O2 | O3 | O4 | |
| О1 | ||||
| О2 | ||||
| О3 | ||||
| О4 |
Таблица 17
| O1 | O2 | O3 | O4 | |
| О1 | ||||
| О2 | ||||
| О3 | ||||
| О4 |
Таблица 18
| O1 | O2 | O3 | O4 | |
| О1 | ||||
| О2 | ||||
| О3 | ||||
| О4 |
Таблица 19
| O1 | O2 | O3 | O4 | |
| О1 | ||||
| О2 | ||||
| О3 | ||||
| О4 |
Таблица 20
| O1 | O2 | O3 | O4 | |
| О1 | ||||
| О2 | ||||
| О3 | ||||
| О4 |
В матрице, представленной в таблице (19), дана сумма матриц (таблицы 14-19) в соответствии с вычислениями величин aik по формуле (26). По формуле (26), что число экспертов d = 5, получаем порог d / 2 = 2,5 и сравниваем все элементы aik в последней таблице (19) с порогом 2,5. Если aik > 2,5, то проставляем Jik* = 0. Результатом сравнения элементов матрицы || aik || с порогом 2,5 представляем в обобщенной матрице парных сравнений, изображенной в таблице 20.
Для построения обобщенной ранжировки объектов по матрице парных сравнений вычислим коэффициенты весов всех объектов. Для первого приближения t = 1 имеем по формуле (51)
 ,
, 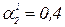 ,
,  ,
,  .
.
По значениям коэффициентов ранжируем объекты
 O2 O1 O4 O3
O2 O1 O4 O3
Вычислим коэффициенты весов для второго приближения t = 2, используя коэффициенты первого приближения.
Упорядочение объектов по этим коэффициентам соответствует упорядочению по коэффициентам первого приближения, т.е. оно не изменилось.
Таким образом, обобщенной ранжировкой четырех объектов по результатам индивидуальных ранжировок экспертов является ранжировка
 O2 O1 O4 O3
O2 O1 O4 O3
Построим теперь обобщенную ранжировку способом сумм рангов. Для этого просуммируем ранги для каждого объекта, используя таблицу (13). В результате получаем
О1 =10; O2 = 8; O3 = 17; O4 = 15.
Отсюда следует упорядочение объектов О1 =10; O2 = 8; O3 = 17; O4 = 15, которое совпадает с упорядочением, полученным в предыдущем случае, т.е.
 O2 O1 O4 O3
O2 O1 O4 O3
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1458; Нарушение авторских прав?; Мы поможем в написании вашей работы!