Метод фазовых траекторий для линейных систем

Как известно, в линейных системах второго порядка возможны следующие переходные процессы:

1. Устойчивые:

a. колебательный;

b. апериодический.

2. Неустойчивые:

a. колебательный;

b. апериодический.

3. Переходные процессы системы, находящейся на границе устойчивости:

a. апериодическая граница устойчивости;

b. колебательная граница устойчивости.

Рассмотрим эти переходные процессы и фазовые траектории, соответствующие данным переходным процессам

Устойчивый колебательный переходный процесс имеет вид:

Рис. 4.32.

Фазовая траектория для данного переходного процесса имеет вид:

Рис. 4.33.

Устойчивый апериодический переходный процесс имеет вид:

Рис. 4.34.

Фазовая траектория для данного переходного процесса имеет вид:

Рис. 4.35.

Неустойчивый колебательный переходный процесс имеет вид:

Рис. 4.36.

Фазовая траектория для данного переходного процесса имеет вид:

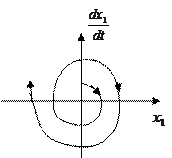Рис. 4.37.

Неустойчивый апериодический переходный процесс имеет вид:

Рис. 4.38.

Фазовая траектория для данного переходного процесса имеет вид:

Рис. 4.39.

Система, находящаяся на границе колебательной устойчивости, имеет переходный процесс:

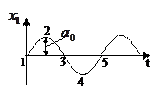Рис. 4.40.

Фазовая траектория для данного переходного процесса имеет вид:

Рис. 4.41.

Рассмотрев фазовые траектории для линейных систем можно сделать следующие выводы:

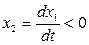§ В верхних квадрантах фазовой плоскости изображающая точка движется всегда слева направо, а в нижних – справа налево. Это объясняется тем, что при переменная возрастает, а при переменная 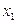убывает.

§ В любой точке фазовой плоскости, где переменная и функция не равны нулю, фазовая траектория имеет только одно определенное направление, соответствующее значению производной в данной точке. Из этого следует, что фазовые траектории в таких точках не пересекаются.

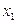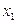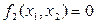§ Если , то , т. е. фазовые траектории пересекают ось под прямым углом, а переменная достигает своего максимума. Если при одновременно , то фазовая траектория в таких точках не имеет определенного направления, а обе производные 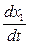и 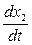равны нулю. (18). Последнее означает, что изображающая точка неподвижна, а исследуемая система управления находится в состоянии равновесия. Такие точки называются особыми.

§ Если переходный процесс является сходящимся, что соответствует устойчивым система, то фазовая траектория имеет вид либо скручивающейся к началу координат спирали (для колебательного процесса), либо дуги, сходящейся к началу координат (для апериодического процесса);

§ Если система неустойчива, то фазовая траектория - раскручивающаяся спираль или расходящаяся дуга;

§ Если в системе установились колебания с постоянной амплитудой и частотой, то фазовой траекторией является эллипс, который называется предельным циклом.. По параметрам эллипса можно определить амплитуду и частоту;

§ Для всех фазовых траекторий характерны следующие особенности: в верхних квадрантах плоскости фазовые траектории имеют направление слева направо; в нижнем квадранте – справа налево

Свойства фазовых траекторий для линейных систем сохраняются и для фазовых траекторий нелинейных систем. Однако фазовые траектории нелинейных систем имеют свои особенности.

4.5.1.3. Особенности нелинейных систем:

§ В нелинейных системах, как правило, рассматривают фазовый портрет системы, т. е. совокупность фазовых траекторий, соответствующих различным начальным условиям.

§ Нелинейные элементы изменяют фазовые траектории, например фазовые траектории нелинейных систем с нелинейностями типа «реле» имеют изломы в линии, называемой линией переключения

Рис. 4.42.

§ Если нелинейный элемент имеет зону нечувствительности, то фазовый портрет нелинейной системы имеет множество особых точек, которые определяют отрезок равновесия.

Рис. 4.43.

§ Режиму автоколебаний соответствует фазовый портрет, на которм фазовые траектории сходятся к предельному циклу.

Рис. 4.44.

§ Для систем устойчивых в малом, но неустойчивых в большом фазовый портрет имеет вид, при котором фазовые траектории, внутри предельного цикла сходятся к началу координат, а вне предельного цикла расходятся от предельного цикла. Предельный цикл в данном случае является неустойчивым.

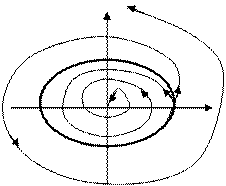Рис. 4.45.

Метод фазовых траекторий графическим методом дает наглядное изображение устойчивости систем и определения режима автоколебания.

В отличие от линейных систем в нелинейных может быть несколько режимов автоколебания, что соответствует нескольким предельным циклам. Параметры предельного цикла определяют параметры автоколебания (амплитуду и частоту). Однако метод фазовых траекторий удобен для исследования систем второго и третьего порядков, поэтому этот метод имеет ограниченное использование.

ПРИМЕР

Построить фазовый портрет для следующей системы

Рис. 4.46.

Где , а нелинейный элемент – реле, имеющий статическую характеристику :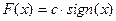

Рис. 4.47.

Уравнение (4.12) можно переписать в виде

(4.27)

Если входной сигнал – единичное ступенчатое воздействие, то (27) принимает вид

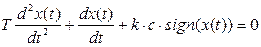(4.28)

Введем новые фазовые переменные:

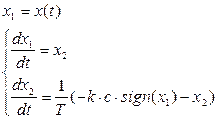(4.29)

Уравнение фазовых траекторий имеет вид:

(4.30)

При 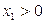уравнение имеет вид:

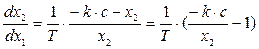(4.31)

При 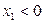уравнение имеет вид:

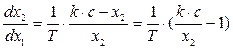(4.32)

Разрешив такие уравнения при заданных начальных условиях можно получить уравнение для фазовых траекторий:

Для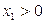

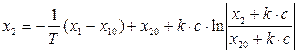(4.33)

Для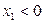

(4.33)

Дата добавления: 2014-01-07