Уравнения идеальной работы акселерометра

(вернуться к оглавлению)

Акселерометр является одним из основных информационных источников который наряду с гироскопическими устройствами позволяют решать задачи навигации автономными средствами. Гироскопы и акселерометры входят в состав комплексных навигационных систем. Акселерометр измеряет кажущееся ускорение.

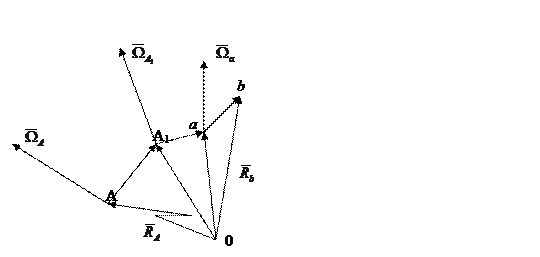
А - центр тяжести ЛА;

R _А - радиус-вектор центра масс ЛА относительно точки – 0 инерциальной системы отсчета;

А₁ – точка приборной платформы, на которой располагаются базовые приборы навигационной системы. В частности, – акселерометры;

а - точка корпуса акселерометра;

в – центр масс ЧЭ акселерометра;

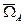- абсолютная угловая скорость объекта относительно инерциального пространства;

- абсолютная угловая скорость приборной платформы;

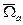- абсолютная угловая скорость корпуса акселерометра.

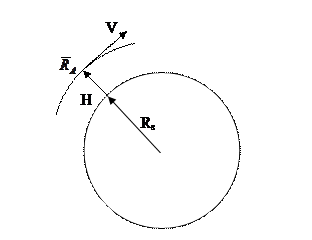
Рис.

Для частного случая облета Земли на высоте H от поверхности соответствующие угловые скорости будут иметь вид:

,

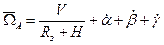где 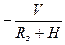, - угловая скорость облета Земли или угловая скорость поворота вертикали места;

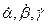- - соответственно угловые скорости тангажа, крена, рысканья ЛА.

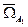- абсолютная угловая скорость приборной площадки. Соотношение между 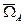и 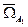зависит от способа связи приборной площадки относительно корпуса самолета.

Если приборная площадка не имеет степеней свободы относительно ЛА (жестко зафиксирована относительно строительных осей), то 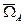=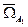. Это – вариант, реализуемый в БИНС – в бесплатформенных инерциальных навигационных системах.

Если приборная площадка размещена на гиростабилизированной платформе, развязанной от угловых движений ЛА относительно центра масс – А, то в зависимости от того, как ориентированы оси приборной платформы относительно базовых направлений пространства, могут быть различные варианты. В частности, оси платформы могут занимать неизменные направления в инерциальном пространстве (в астроинерциальных системах). Тогда 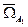= 0.

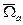- абсолютная угловая скорость корпуса акселератора. Если корпус акселерометра жестко зафиксирован на приборной площадке, то 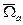=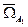. Но в некоторых случаях требуется реализовать акселерометр, с так называемым, следящим корпусом. Корпус акселерометра принудительно отрабатывается в положение, при котором выходной сигнал U ₁ датчика угла близок к нулю. Суммарный выходной сигнал такого акселерометра формируется как сумма сигнала смещения корпуса и сигнала узкодиапазонного датчика угла смещения ЧЭ акселерометра. И тогда - ≠.

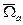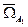, (1)

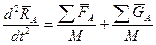, (2),

- абсолютное ускорение центра масс ЛА,

где

- - сумма активных сил на ЛА;

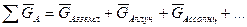- - сумма гравитационных сил на ЛА;

В свою очередь абсолютное ускорение точки b ЧЭ определится из уравнения (1):

(3)

Разрешив это уравнение относительно 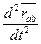с учетом (1) и (2) получим:

(4)

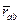- абсолютное и 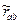- относительное смещение ЧЭ относительно корпуса.

- абсолютные ускорения соответственно точек A₁ платформы и a корпуса акселерометра.

Приложение.

Дифференцирование радиуса-вектора точки в произвольном движении.

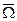Дано: радиус – вектор произвольной точки. - его абсолютная угловая скорость.

Абсолютная производная радиуса-вектора примет вид:

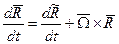(5),

Здесь - , относительная скорость точки, характеризующая изменение длины радиуса-вектора;

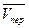- = , переносная скорость, учитывающая его вращение.

Продифференцировав (5) еще раз, получим:

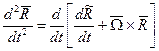(6)

Применив к (6) формальное правило дифференцирования вектора, стоящего в квадратной скобке, аналогично (5) можно получить выражение для абсолютного ускорения точки.

(дополнить, комментарий для составляющих абс. ускорения)

Если выявленные закономерности применить к соответствующим векторам выражения (3) и разрешить векторное уравнение относительно 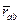, в котором присутствует наблюдаемая компонента 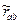, получим:

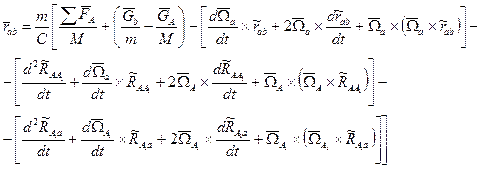
Дата добавления: 2014-01-07