Зображення земної поверхні на планах та картах

Фізична поверхня Землі досить складна. Для її вивчення і для розв’язання практичних і інженерних задач її зображають на планах та картах.

При складанні карт та планів сферичну поверхню Землі методом ортогонального проектування переносять на горизонтальну площину Р (рис. 2.1).Лінії проектування Аа, Вb, Cc повинні бути перпендикулярними до проектної площини. Великі за площею ділянки земної поверхні проектують на поверхню референц-еліпсоїда.

Рис. 2.1. Метод ортогонального проектування точок місцевості

Різниця між довжиною лінії АВ на поверхні сфероїда та її довжиною АВ ' на площині визначається за формулою

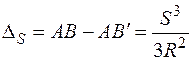. (2.1)

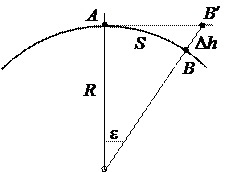При довжині дуги АВ в 10 км величина D_S < 10 см.

Рис. 2.2. Вплив сферичності Землі на довжину ліній та висоти точок

Спотворення висоти за кривизну Землі визначиться за формулою

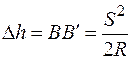. (2.2)

При R = 6371 км і d_AB = 1 км, D h = 78,5 мм, а при S = 100м, D h = 0,8 мм

Лінії аb,bc,ca називають горизонтальними прокладаннями ліній місцевості АВ, ВС, СА. При визначеному куту нахилу n лінії АВ горизонтальне прокладання обчислюють за формулою

.

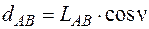Отримане на площині зменшене зображення земної поверхні із збереженням подібності фігур ситуації і рельєфу називають планом місцевості.

Ступінь зменшення горизонтальних прокладань ліній місцевості при зображені їх на плані або карті називається масштабом.

План – це зменшене подібне зображення невеликої ділянки місцевості без врахування кривизни Землі.

Карта – це зменшене узагальнене зображення на площині всієї поверхні Землі або значних її територій з врахуванням кривизни Землі.

Для зображення сферичної поверхні Землі на площині без розривів виконують досить складні математичні розрахунки так званих картографічних проекцій. При цьому мережу меридіанів і паралелей з поверхні сфероїда переносять на поверхню циліндра або конуса, яку потім розгортають в площину.

Земну поверхню можна перетнути вертикальною площиною.

Побудоване на площині за певними правилами зображення сліду перетину рельєфа земної поверхні вертикальною площиною називають профілем місцевості.

Карти і плани повинні бути точними, подібними, достовірними та в повній мірі відображати земну поверхню.

6. Зональна система плоских прямокутних координат Гауса - Крюгера

Карти та плани складають на площині. Поверхню еліпсоїда неможливо розгорнути на площину без спотворень. Тому розроблені картографічні проекції дозволяють математичними розрахунками геодезичні (географічні) координати В та L точок еліпсоїда переобчислити в прямокутні координати Х та Y.

Така проекція була розроблена К.Ф.Гауссом та Л.Крюгером і отримала назву: система плоских прямокутних координат Гаусса-Крюгера.

Якщо земну кулю обгорнути циліндром, то отримаємо лінію їх дотику по меридіану РР ₁ (рис.2.3, а).

З центру Землі точки 0 поверхню еліпсоїда по довготі в 6^о проектують на поверхню циліндра, яку потім можна розвернути в площину (рис.2.3, б). Аналогічно можна спроектувати на поверхню циліндра всю поверхню еліпсоїда, отримавши 60 зон.

а б

Рис. 2.3 Схема побудови зональної системи плоских прямокутних координат

Вісь абсцис Х утворює середній меридіан в кожній зоні. Зображення екватора в вигляді прямої перпендикулярної осьвому меридіану приймають за вісь ординат Y.

Координати Х на північ від екватора мають знак плюс (+ Х), а на південь – мінус (- Х). Ординати Y в кожній зоні обчислюють з плюсом (+ Y) на схід від осьового меридіану, на захід – з мінусом (- Y).

Для зручності початок координат в кожній зоні збільшують на 500 км (рис. 2.4) внаслідок чого вони будуть позитивними. Щоб визначити зону, в якій знаходиться шукана точка, попереду значення кожної ординати вказують номер зони. Наприклад, для точки А (рис.2.4) маємо Х = 2845341 м; Y = 3824152 м. Це означає, що точка знаходиться в 3-й зоні, а її ордината фактично дорівнює Y = 824152 – 500 000 = 324152 м і знаходиться на схід від осьового меридіану.

Рис. 2.4. Координатна сітка

Ординати в умовних значеннях (рис. 2.4) обчислюються за формулою

;

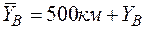. (2.3)

При вирішенні ряду відповідальних інженерних задач в будівництві використовують 3^о – ні зони. Спотворення ліній на лінії осьового меридіану відсутні і зростають в напрямку до краю зони.

При цьому за осьовий меридіан приймають умовний меридіан, що проходить через центр будівельного майданчика.

Величину поправки D s в довжину лінії S на площині можна визначити за формулою

, (2.4)

де 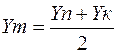, Yп, Yк – координати початкової та кінцевої точок лінії; R = 6371 км – середній радіус сфероїда.

Для зручності визначення прямокутних координат на планах і картах нанесена координатна сітка (Рис. 2.4). Це система взаємоперпендикулярних ліній проведена через певні відстані паралельно осям х та у зони. Значення абсцис х та умовних ординат у ліній координатної сітки підписані на картах та планах.

Дата добавления: 2014-01-07