Применение метода гармонической линеаризации для определения режима автоколебаний

Применяя гармоническую линеаризацию на вышеприведенных допущениях можно исследовать устойчивость системы методами теории устойчивости линейных систем.

Рассмотрим типовую нелинейную систему. Передаточная функция линейной части имеет вид:

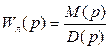(4.48)

Эквивалентную передаточную функцию нелинейного элемента можно получит из (47):

(4.49)

Тогда передаточная функция замкнутой системы имеет вид:

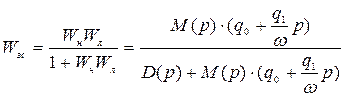(4.50)

А характеристическое уравнение гармонически линеаризованной системы имеет вид:

(4.51)

Наиболее удобно исследовать автоколебания при помощи критерия Михайлова:

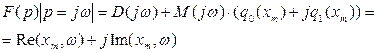(4.52)

Согласно критерию устойчивости Михайлова в системе установятся колебания с постоянной амплитудой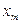и частотой , если годограф Михайлова проходит через начало координат, т. е. когда и мнимая и действительная части характеристического полинома одновременно равны нулю:

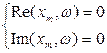(4.53)

Разрешая данную систему уравнений относительно , можно определить возможность возникновения автоколебаний в системе. Если уравнения (4.53) не имеют положительных корней, то автоколебания в системе невозможны.

Если положительные величины, то системе возможен режим колебания с постоянной амплитудой. Определить, являются ли данные колебания автоколебаниями, можно с помощью дополнительных исследований.

Изучая фазовые траектории, соответствующие режиму автоколебаний, можно сделать следующий вывод: что в режиме автоколебаний при увеличении амплитуды 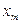на величину 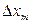в системе происходил сходящийся процесс к величине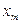; а при уменьшении на 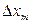происходил расходящийся процесс до величины 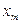. Аналогичные процессы происходят при изменении частоты .

Для дополнительных исследований на устойчивость колебаний применяются критерии устойчивости: Гурвица, Михайлова и Найквиста.

Дата добавления: 2014-01-07