Критерий Найквиста. Согласно критерию Найквиста система находится на колебательной границе устойчивости, если амплитудно-фазовая характеристика разомкнутого контура проходит

Согласно критерию Найквиста система находится на колебательной границе устойчивости, если амплитудно-фазовая характеристика разомкнутого контура проходит через точку 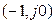. Следовательно, условием существования автоколебаний является равенство:

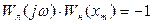(4.58)

или

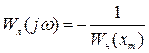(4.59)

Левая часть уравнения (4.59) представляет собой АФХ линейной части, а правя – обратную характеристику нелинейного элемента, взятую с противоположным знаком.

Уравнение (4.59) можно решить графически. Строится два графика 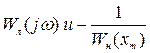, точки пересечения этих графиков определяют режимы колебаний с постоянной амплитудой и частотой.

Для определения режима автоколебаний пользуются следующим правилом:

Если точка на графике 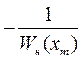, близкая к точке пересечения, но сдвинутая в сторону увеличения параметра 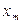не охватывается графиком 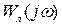, то колебания являются устойчивыми, в противном случае – неустойчивыми.

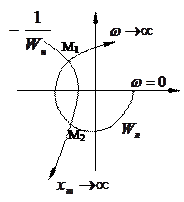Рис. 4.49.

На рисунке точка М₁ соответствуют режиму автоколебаний, а М₂ – неустойчивым колебаниям.

ПРИМЕР

Пусть дана нелинейная система:

Рис. 4.50.

Параметры системы:

Линейная часть представлена 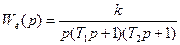, где k=0.4; T₁=1 c; T₂=5 c.

Нелинейный элемент имеет характеристику

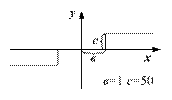
Рис. 4.51.

Определить есть ли в данной системе автоколебания. Если есть, то найти параметры входного воздействия, при котором в системе наблюдаются автоколебания.

Применим метод гармонической линеаризации:

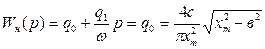
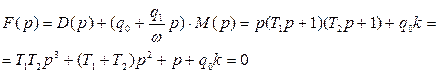
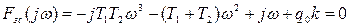
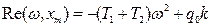
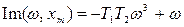
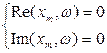
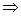
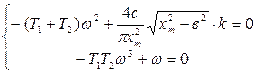
Найдем значение x_m, ω.:

Из второго уравнения системы имеем:

=>

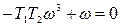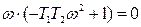
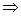
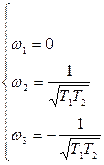
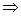
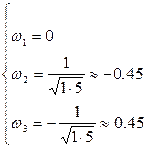
В системе возможны автоколебания при ω> 0, значит, они возможны только при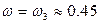

Из первого уравнения системы найдем x_m, соответствующие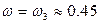

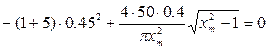
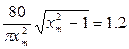
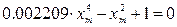
Разрешив биквадратное уравнение через замену переменной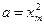

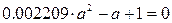
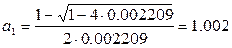
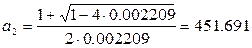
Получаем четыре корня:

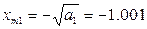
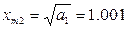
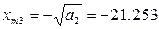
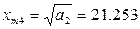
Очевидно, что при всех x _m ограничения (1), (2) выполняются, при x _m ≤0 в системе автоколебаний быть не может. Получилось 2 решения системы: (0.45;1.001) и (0.45;21.253). Для дополнительных исследований используем критерий Михайлова:

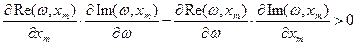
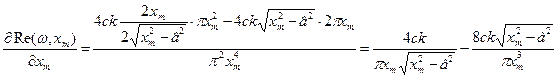
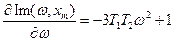
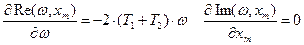
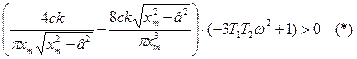
Проверим, выполняется ли неравенство (*) для полученных решений:

а). При ω =0.45 x _m=1.001

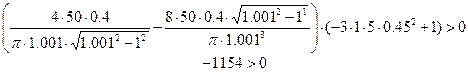
Как видно неравенство не выполняется, значит, при данных значениях в системе автоколебаний не будет.

б). При ω =0.45 x _m=21.253

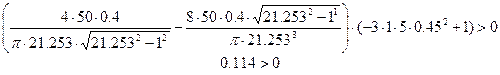
Неравенство выполняется, значит, при данных значениях входного сигнала в системе будут наблюдаться автоколебания. Промоделируем эту схему в MATLAB 5.1.

Полученная схема:

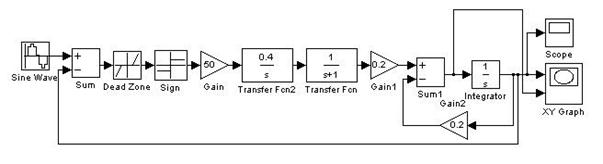
Рис. 4.52.

Выходной сигнал системы при значениях входного сигнала ω =0.45 x _m=21.253:

Рис. 4.53.

Фазовая траектория:

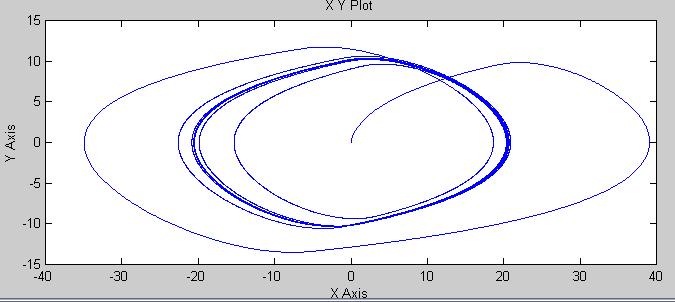
Рис. 4.54.

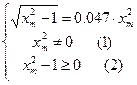
Дата добавления: 2014-01-07