Молекулярно-кинетические свойства дисперсных систем

Молекулярно-кинетические свойства коллоидных систем и растворов ВМС, как и газов, и молекулярных или ионных растворов, обнаруживаются в таких явлениях, как броуновское движение, диффузия, осмотическое давление, седиментация. Частицы ультрамикрогетерогенных систем (золей, аэрозолей) участвуют в тепловом движении и подчиняются всем молекулярно-кинетическим законам. Благодаря этому можно экспериментально определить размер, массу и концентрацию частиц дисперсной фазы.

К молекулярно-кинетическим свойствам (определяемым размерами частиц и их проявляющимися при движении) относят диффузию, осмос, броуновское движение и седиментацию.

1. Диффузия - это самопроизвольный процесс выравнивания концентрации частиц во всем объеме коллоидной системы или молекул в растворах.

Еще Т. Грэм в 1861 г. показал, что коллоидные частицы диффундируют гораздо медленнее, чем молекулы в истинных растворах низкомолекулярных веществ. Позднее было установлено, что причиной этой характерной особенности лиозолей является большой размер коллоидных частиц по сравнению с молекулами. Со временем, после разработки точных приборов для определения концентрации дисперсной фазы, измерение коэффициента диффузии частиц в лиозолях превратилось в один из основных методов коллоидной химии, предназначенных для определения размеров частиц дисперсной фазы.

Во всех случаях диффузия идет из слоя золя с более высокой концентрацией частиц до полного выравнивания их концентраций во всех частях системы. Если обозначить dm количество вещества, перенесенного через сечение S по направлению x за время dt, то в соответствии с первым законом А. Фика

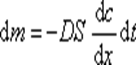
где D – коэффициент диффузии; dc/dx – градиент концентрации, S- площадь поверхности, через которую диффундируют частицы.

Знак «минус» показывает, что процесс идет в сторону уменьшения концентрации.

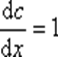Если S=1 и

то

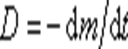
т.е. коэффициент диффузии — это масса вещества, продиффундировавшего за единицу времени через единицу площади при градиенте концентрации, равном единице.

Закон Фика приобретает особенно простой вид, если ввести понятие диффузионного потока, определяемого как количество вещества, перенесенного за единицу времени через сечение, равное единице, т.е.

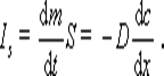
Из входящих в закон Фика величин только одна зависит от свойств диспергированного вещества и дисперсионной среды – это коэффициент диффузии D.

Диффузия очень медленный процесс, поэтому D также мал. Наиболее высокие значения D присущи газам, подвижность частиц которых наибольшая.

Коэффициент диффузии коллоидных частиц определяется из уравнения Эйнштейна

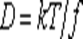
где k – постоянная Больцмана; f – коэффициент трения коллоидной частицы о вещество дисперсионной среды.

Для сферических несжимаемых частиц, движущихся бесконечно медленно с постоянной скоростью в непрерывной несжимаемой среде так, что жидкость не скользит на поверхности частиц, по закону Стокса:

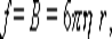
где η – вязкость среды; r – радиус частиц.

Таким образом

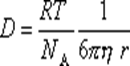
Из этого уравнения, полученного Эйнштейном в 1905 г., видно, что коэффициент диффузии D и скорость диффузии dm/dt не зависят от массы частиц, так как она (масса) не входит в эти уравнения, но зависят от размеров частиц.

Пользуясь уравнением Эйнштейна, можно определить радиус частиц:

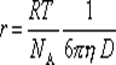
Перрен использовал это уравнение для определения молекулярной массы ряда веществ в истинных растворах и получил достаточно хорошо согласующиеся с теоретическими данными результаты. Таким образом, он доказал, что закон Стокса применим и к молекулярным системам. Однако «молекулярно-частичная» масса коллоидов по этой формуле определяется гораздо точнее, чем молекулярная масса веществ в истинных растворах.

Если рассматривать диффузию частиц в аэрозолях, то оказывается, что закон Стокса в некоторых случаях неприменим, поэтому в уравнение для коэффициентов диффузии необходимо вводить поправки.

Постоянная Стокса В для частиц в аэрозолях меняется в зависимости от размера частиц r.

Существует ряд методов непосредственного определения коэффициента диффузии D экспериментальным путем. Все эти методы основаны на приведении в контакт чистого растворителя (дисперсионной среды) с раствором (золем), тщательном термостатировании, последующем отборе проб без перемешивания системы и их анализе. На основании этих данных определяют dc/dx и рассчитывают D.

Дата добавления: 2014-01-07