Броуновское движение

Броуновское движение (название дано в честь английского ботаника Броуна, обнаружившего с помощью микроскопа непрерывное движение мелких частичек цветочной пыльцы, взвешенных в воде) проявляется в хаотическом и непрерывном движении частиц дисперсной фазы под действием ударов молекул растворителя (дисперсионной среды), находящихся в состоянии интенсивного теплового движения. В зависимости от размера частиц их движение может быть различным. Частицы коллоидной степени дисперсности, испытывая с разных сторон многочисленные удары молекул жидкости, могут перемещаться поступательно в самых разнообразных направлениях. Траектория движения таких частиц представляет собой ломаную линию совершенно неопределенной конфигурации. Перемещение частиц фиксируют, например, с помощью микросъемки.

Количественной мерой перемещения частицы при броуновском движении является величина среднего смещения (или сдвига) частицы Δ за некоторый промежуток времени t. Смещением или сдвигом частицы называют расстояние между проекциями начальной и конечной точек траектории на ось в выбранном направлении. Поскольку перемещение частиц может происходить в любом направлении, его характеризуют среднеквадратичным значением

Молекулярно-кинетические расчеты показывают, что коллоидные частицы способны проделывать элементарный путь l длиной 4·10-10 мза время 3·10-10 с.

В 1903 г. Р. Зигмонди сконструировал ультрамикроскоп и с его помощью установил, что мелкие частицы находятся в еще более, чем крупные, интенсивном движении. Эти частицы не только колеблются около одного центра, но и совершают зигзагообразное движение. Движение крупных частиц более сложно, чем мелких, так как масса такой частицы намного превосходит массу молекул и, следовательно, каждое столкновение с движущимися молекулами отклоняет частицу на ничтожно малое расстояние.

Даже при наблюдении в ультрамикроскоп можно увидеть только суммарные пути за определенный промежуток времени. Наименьшее наблюдаемое человеком время 0,1 с, поэтому путь, составляющий длину пробега частицы, равен 107l, т.е. 10 млн. элементарных движений, следовательно, возможность наблюде­ния элементарного пути исключается. Поэтому рассматривают средний сдвиг частицы

где xi– элементарное смещение частицы по оси x. где n – число смещений (число отрезков ломаной линии); Δ i – отдельные проекции смещения частицы на ось.

В 1905-1908 гг. А. Эйнштейн и М. Смолуховский независимо друг от друга разработали теорию броуновского движения. В основе теории заложены следующие предпосылки:

– кинетическая энергия частицы, взвешенной в жидкости или газе, соответствует средней кинетической энергии молекул;

- экспериментатор может не считаться с фактически пройденным частицей путем или с фактической скоростью частицы, он может ограничиться средним смещением частицы за определенное время.

Из уравнения Эйнштейна-Смолуховского следует, что величина Δ² обратно пропорциональна радиусу частицы r. Это означает, что чем крупнее частица, тем меньше величина ее смещения. С увеличением размера частиц прежде всего прекращается поступательное броуновское движение, затем исчезает вращательное движение и остается колебательное.

3. Осмос. Механизм и основные закономерности осмоса рассматриваются в курсе физической химии. Поэтому здесь достаточно напомнить, что при разделении двух растворов различной концентрации (или раствора и чистого растворителя) полупроницаемой мембраной возникает поток растворителя от раствора с меньшей концентрацией к большей, выравнивающий концентрации. В дальнейшем поток уравновешивается возникающим встречным градиентом давления. Этот процесс обусловлен, в термодинамической трактовке, ростом энтропии системы, а в кинетической, – избыточным числом ударов молекул растворителя о мембрану со стороны более разбавленного раствора.

Равновесное осмотическое давление для растворов неэлектролитов рассчитывают на основании закона Вант-Гоффа по уравнению

π = cRT,

где c – молярная концентрация.

Применимо ли это уравнение к коллоидным растворам? Для ответа на этот вопрос необходимо прежде всего определить понятие концентрации дисперсной системы. Поскольку речь идет о кинетических явлениях, концентрацией следует считать число кинетических единиц – коллоидных частиц – в единице объема системы, то есть ввести понятие частичной концентрации дисперсной фазы ν.

Следовательно, осмотическое давление пропорционально числу частиц растворенного или диспергированного вещества в единице объема раствора и не зависит от природы и массы частиц. Частичные концентрации коллоидных растворов обычно очень малы по сравнению с растворами молекулярными. Поэтому и величины π коллоидных растворов столь же малы. Таким образом, в отношении осмоса не обнаруживается никаких принципиальных качественных различий между коллоидными и молекулярными растворами; основные закономерности едины, но большие количественные различия в величине концентрации приводят к слабому проявлению осмоса в коллоидных системах. Для количественного изучения осмотического давления применяют специальные приборы – осмометры.

В истинных растворах, отделенных от растворителя полупроницаемой перегородкой, может быть измерено осмотическое давление, величина которого зависит от концентрации растворенного вещества и для разбавленных растворов описывается уравнением Вант Гоффа

где С – массовая концентрация, кг/м3.

Для коллоидных систем можем записать

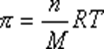
где n – частичная концентрация частиц/м3.

Грэм пытался определить осмотическое давление коллоидных растворов и пришел к ошибочному выводу, что коллоидные системы этим свойством не обладают. Как известно, именно на этом ошибочном факте Грэм провел разделение на истинные растворы и коллоидные системы.

Однако тот факт, что частицы в коллоидном состоянии также совершают хаотическое движение, не оставляет сомнений в том, что осмотическое давление должно быть и у коллоидных систем.

Из уравнения следует, что осмотическое давление пропорционально частичной концентрации. Число частиц в коллоидной системе очень мало по сравнению с истинным раствором, поэтому осмотическое давление золей тоже очень мало. Например,1%-ный золь золота с частичками r» 10-9м имеет осмотическое давление p = 3,45 Па. Чтобы этот золь имел такое же осмотическое давление, как 1М-раствор электролита, понадобилось бы в 1 дм3 диспергировать 50 кг золота с частичками r = 10-9 м.

Очевидно, что при малом осмотическом давлении золя даже малейшая примесь электролита будет оказывать колоссальное влияние на осмотическое давление, поэтому при изучении осмоса в золях их требуется тщательно очищать.

Смолуховский показал, что при изменении степени дисперсности коллоида осмотическое давление обратно пропорционально r3частиц, т.е.

p₁/p₂= (r₂/r₁)3.

4. Седиментация. Или оседание в поле действия силы тяжести.

Седиментацией (от лат. sedimentum – осадок) называют процесс оседания частиц дисперсной фазы в жидкой или газообразной среде под действие силы тяжести. Всплывание частиц (например, капель в эмульсиях) носит название обратной седиментации.

Скорость оседания частиц не зависит от их природы, а определяется размером частиц, разностью плотностей частиц ρ и среды ρ₀ и вязкостью среды η.

В вязкой и плотной среде при седиментации частица движется под действием силы тяжести в гравитационном поле. Сила сопротивления среды, действующая на сферическую частицу, зависит от ее размера, скорости движения, вязкости среды. Сила тяжести, действующая на частицу, равна кажущейся массе,

где g – ускорение свободного падения.

Движение частиц будет направлено вниз, если разность плотностей дисперсной фазы r₂и дисперсионной среды r₁(Δr) положительна, и частицы будут всплывать при Δr<0. Под действием силы Р частицы приходят в равномерно ускоренное движение. Но так как, кроме силы тяжести, на них действует сила сопротивления среды, направленная противоположно и возрастающая пропорционально скорости, то очень скоро сила сопротивления среды уравновешивает силу тяжести, благодаря этому далее движение идет равномерно со скоростью U.

Если экспериментально определить скорость седиментации, то можно рассчитать радиус частиц; так как при стационарном режиме осаждения F = P.

Поэтому

Уравнение Стокса справедливо при соблюдении ряда условий, которые не всегда соблюдаются в реальных системах:

1. Частицы должны быть сферическими. Это условие обычно выполняется для разбавленных эмульсий и частиц полимеров, полученных методом эмульсионной полимеризации. Частицы суспензий часто отклоняются от сферической формы, поэтому для них определяется некоторый эффективный радиус частицы той же массы, движущейся с той же скоростью. Такой радиус называют эквивалентным или эффективным.

2. Отсутствие взаимодействия между частицами. Расстояние между частицами должно быть достаточно большим, чтобы падение одних частиц не сказывалось на скорости других. Поэтому анализ следует проводить при невысоких концентрациях (1-2%).

3. Необходимо, чтобы сосуд, в котором происходит седиментация, был намного больше размеров частиц. Это необходимо для того, чтобы можно было пренебречь влиянием стенок, так как вблизи стенок скорость оседания не следует закону Стокса.

4. Движущиеся частицы должны быть твердыми и гладкими. Это условие связано с возможностью изменения формы частиц в результате возникновения в них микропотоков. Условие не выполняется при течении эмульсий.

5. Отсутствие проскальзывания между оседающей частицей и средой. Необходимо, чтобы частица хорошо смачивалась жидкостью, так как в уравнение входит вязкость именно жидкости.

6. Скорость оседания должна быть постоянной, иначе сила тяжести не уравновесится силой трения.

7. Скорость оседания должна быть небольшой, в противном случае возникает турбулентный режим течения, и тогда нельзя будет использовать вязкость h, соответствующую ламинарному режиму

Дата добавления: 2014-01-07