
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция №2
|
|
|
|
Обозначим число таких молекул 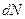 . Тогда
. Тогда
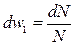 ,
,
где 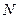 – число молекул в этом объеме.
– число молекул в этом объеме.
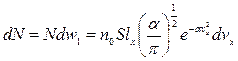 ,
,
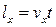 .
.
Давление, которые создают эти молекул
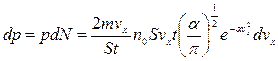 .
.
За этот же промежуток времени  о грань
о грань 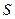 ударяют молекулы и с другими скоростями. Поэтому давление от всех молекул
ударяют молекулы и с другими скоростями. Поэтому давление от всех молекул
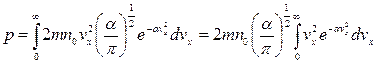 .
.
Для решения этого интеграла воспользуемся интегралом Пуассона
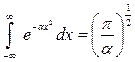 .
.
Это выражение можно рассмотреть как функцию  . Возьмем производную по этому параметру
. Возьмем производную по этому параметру
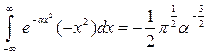 .
.
Учитывая, что подынтегральная функция четная, можно записать
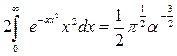 .
.
Тогда
 ,
,
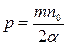 .
.
В курсе школьной и общей физики рассматривается самостоятельно молекулярно-кинетическая теория. В этой модели есть определение давления, температуры.
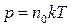 .
.
Приравняем полученное выражение для давления с выражением для давления в молекулярно-кинетической теории и выразим 
 .
.
Параметр  отражает свойства молекулы, а именно маску и свойства окружающей среды – температура.
отражает свойства молекулы, а именно маску и свойства окружающей среды – температура.
Таким образом, функция распределения Максвелла полностью определена.
Найти среднее значение  (квадрат модуля).
(квадрат модуля).
Для решения этой задачи необходимо знать функцию распределения по модулю скоростей. Для её решения целесообразно перейти в сферическую систему координат пространства скоростей.

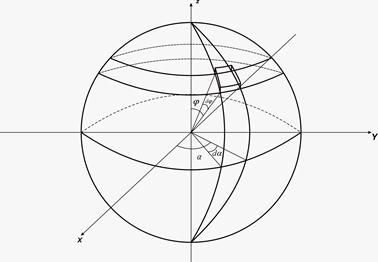

В пространстве v роль полярного радиуса выполняет модуль вектора v.
 - проинтегрируем по
- проинтегрируем по 
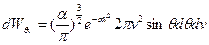

Полученное выражение  - вероятность того, что модуль скорости произвольно выбранной молекулы попадает в промежуток
- вероятность того, что модуль скорости произвольно выбранной молекулы попадает в промежуток 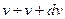 . Т.е. в тонкий шаровой слой толщиной
. Т.е. в тонкий шаровой слой толщиной 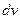 . Это и есть то, что мы искали.
. Это и есть то, что мы искали.
Искомая функция распределения по модулю v.
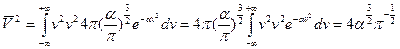


|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 273; Нарушение авторских прав?; Мы поможем в написании вашей работы!