
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Закон исключенного третьего
|
|
|
|
Основные понятия алгебры логики
Алгебра логики (алгебра Буля)
Алгебра логики изучает связь между переменными параметрами, принимающими только два значения:
"1" - логическая единица или "0" - логический нуль.
Если х ¹ 1, то х = 0, если х ¹ 0, то х = 1.
Логическая функция у=f(х1,х2,...,хn) задана, когда каждому набору х однозначно сопоставляется у. Количество функций, образуемых n переменными равно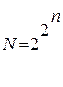 .
.
Если n = 1, то N = 4: у1 = 0,
у2 = 1,
у3 = х,
у4 = /х.
Для двух переменных n = 2 и N = 16.
В таблице 6 приведены некоторые из возможных функций при n=2
| х1 | х2 | у1 | у2 | у3 | у4 |
Таблица 6 – Логические функции двух переменных
6.1.3. Аксиомы алгебры логики
| х+0=х | х×0=0 | х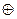 0=х 0=х
|
| х+1=1 | х×1=х | х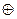 1=х 1=х
|
| х+х=х | х×х=х | х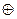 х=0 х=0
|
| х+х=1 | х×х=0 | х х=1 х=1
|
Таблица 7 – Аксиомы алгебры логики
Их можно проверить подставляя вместо х 0 или 1.
6.2.4. Правила Де-Моргана:
Любые логические функции могут быть построены с использованием только элементов "И-НЕ" или только элементов "ИЛИ-НЕ". Переход от операции "И" к операции "ИЛИ", а также обратный переход осуществляется с помощью законов дуальности (теорема де Моргана):
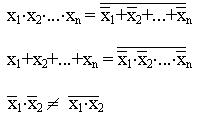
В предыдущей строке показана типичная ошибка,когда полагают,что произведение инверсий равно инверсии произведения этих же переменных.
Закон поглощения
х1+х1×х2 = х1(1+х2) = х1×1 = х1 х1 “поглощает” х2
6.2.5. Минимизация путем алгебраических преобразований
Пусть функция задана в виде таблицы:
| х1 | х2 | х3 | У |
Таблица 8 – Функция, заданная в виде таблицы
Каждая строка таблицы представляет собой конъюнкцию переменных. Если значение переменной в данной строке равно 0, то переменная берется с инверсией.
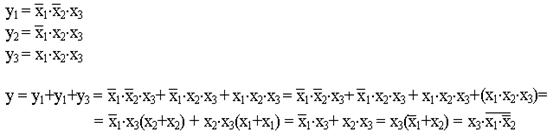
Реализация полученного выражения с помощью элементов ”2и-не”:
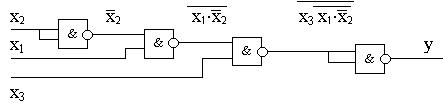
Рисунок 2.5 – Реализация функции, заданной таблицей
6.1.6. Минимизация с помощью диаграмм Карно
Правило построения диаграммы Карно
Для n переменных заполняется прямоугольная таблица, содержащая 2n клеток так, чтобы в соседних клетках конъюнкции отличались не более, чем одним сомножителем.
Если минимизируемая функция при данном наборе переменных равна 1, то в соответствующую клетку ставится 1 (нули можно не ставить). В прямоугольной таблице единицы обводятся контурами и записывается функция в виде суммы произведений, описывающих контуры. Число клеток внутри контура 2к (1,2,4,8...).
Следует покрыть все единицы возможно меньшим числом возможно более крупных блоков. Каждому блоку сопоставляется конъюнкция, записываемая следующим образом:
1)Если блок целиком лежит в единичной области переменной хi, то она включается в конъюнкцию без инверсии, если в нулевой области, то с инверсией.
2) Если блок делится точно пополам между нулевой и единичной областями хi,то хi в конъюнкцию не включается (склеивание по хi).
Других расположений правильно выбранного блока быть не может.
Например:
а) для двух переменных,заданных таблицей

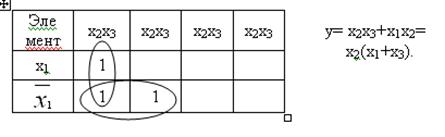
б) для трех переменных:
6.3. Цифровые коды
6.3.1. Двоичный позиционный код
В обыденной жизни применяется десятичная система счисления, в которой используется 10 цифр от 0 до 9 и число представлено как сумма степеней числа 10. Например, число 1407 представляет сокращенную запись суммы 1*103 +4*102 +0*101 +7*100. В цифровой электронике чаще всего используется двоичная система счисления.
Двоичная (бинарная) система основана на степенях числа 2, оперирует только с двумя символами (цифрами): 0 и 1. Двоичная цифра (символ 0 и 1) является единичной элементарной информацией, которая называется битом. Биты объединяются в слова определенной длины, слово длиною в 8 бит называется байтом, В настоящее время наиболее распространены системы с байтовой организацией данных. Поскольку в двоичной системе используется два символа, она имеет основание 2 и значения, которые должны быть приписаны отдельным позициям (веса), являются степенями числа 2.
Целые числа без знака в двоичной системе счисления представляются следующим образом:
am2m+am-12m-1+....+a4 24+a3 23+a2 22+a1 21+a0 2°,где ai=0,или 1
Наименьшая значащая цифра (младший разряд числа) здесь расположена справа, а слева последовательно каждая цифра представляет собой более высокий разряд, более высокую степень числа 2. Например, код 1011 представляет число
1*23+0*22+1*21+1*20=8+2+1=11
При сдвиге целого числа на одну позицию влево производится умножение на два, а при сдвиге на одну позицию вправо производится деление на 2, что обусловлено основанием этой системы счисления.
Перевод чисел из двоичной системы счисления в десятичную
Перевод выполняется путем сложения весов тех разрядов, в которых имеются единицы. Например:
Веса 27 26 25 24 23 22 21 20
Переводимое число 1 0 0 1 1 0 1 1
= 128 + 0 + 0 + 16 +8 + 0 + 2 + 1 =155
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 369; Нарушение авторских прав?; Мы поможем в написании вашей работы!