
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дифференциальные уравнения равновесия покоящейся жидкости
|
|
|
|
Абсолютный и относительный покой.

Дифференциальные уравнения равновесия покоящейся жидкости иначе называют дифференциальными уравнениями Эйлера. Они получены для общего случая относительного покоя жидкости. Возможны следующие варианты относительного покоя.
Первый вариант соответствует абсолютному покою или равномерному движению сосуда с жидкостью. Такой вариант рассматривался при выводе основного уравнения гидростатики.
Второй вариант – вращение сосуда с жидкостью с постоянной угловой скоростью ω вокруг центральной оси. Несмотря на то, что вся масса жидкости вращается вместе с сосудом, частицы жидкости друг относительно друга не перемещаются, следовательно, весь объём жидкости, как и в первом случае, представляет собой как бы твёрдое тело. Давление в каждой точке жидкости не меняется во времени и зависит только от координат. По этим причинам жидкость подпадает под определение покоящейся.
Третий вариант аналогичен второму, только вращение осуществляется вокруг произвольно расположенной вертикальной оси. Во втором и третьем случае свободная поверхность жидкости принимает новую форму, соответствующую новому равновесному положению жидкости.
В четвёртом варианте сосуд с жидкостью движется прямолинейно и равноускоренно. Такой случай проявляется, например, в процессе разгона или остановки автоцистерны с жидкостью. В этом случае жидкость занимает новое равновесное положение, свободная поверхность приобретает наклонное положение, которое сохраняется до изменения ускорения. Частицы жидкости друг относительно друга находятся в покое, и давление зависит только от координат.
Во всех перечисленных случаях на жидкость действуют, во-первых, силы веса, во-вторых, силы инерции, в-третьих, силы давления.
Рассмотрим в произвольной системе координат X,Y,Z произвольную точку A. Вблизи этой точки выделим элементарный объём 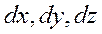 в форме прямоугольного параллелепипеда, грани которого для простоты
в форме прямоугольного параллелепипеда, грани которого для простоты
 |
математических выражений параллельны координатным плоскостям.
Заметим следующее:
ü давление является функцией координат (при этом в любой точке оно по всем направлениям одинаково),
ü при переходе к точкам Ax(Ay, Az) меняется только одна координата на бесконечно малую величину dx(dy, dz), поэтому функция получает приращение только по одной координате,
ü это приращение равно частному дифференциалу по соответствующей координате 


Таким образом, разность давлений, действующих на противоположные грани параллелепипеда (внутрь рассматриваемого объёма), перпендикулярные соответствующим осям, будет иметь вид:
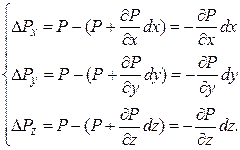
Исходя из этого, определим разности сил, вызванных давлением, в проекции на оси координат
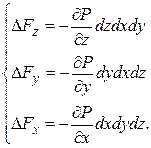
Кроме сил давления на параллелепипед будут действовать инерционные силы  в общем случае определяемые массой и ускорениями ax, ay, az
в общем случае определяемые массой и ускорениями ax, ay, az
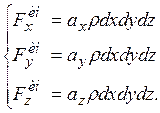
Учитывая, что параллелепипед находится в покое, сумма сил, действующих на него, равна 0:
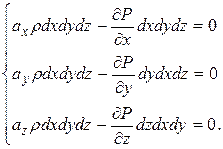
Разделив систему уравнений сил на массу рассматриваемого параллелепипеда, получим систему уравнений Эйлера:

На практике, чтобы избавиться от частных производных, используют одно уравнение, заменяющее систему. Для этого первое уравнение умножают на dx, второе на dy, третье на dz и складывают их:
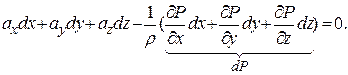
В этой формуле сумма в скобках является полным дифференциалом давления, который в результате оказывается равным

Полученное уравнение показывает, как изменяется давление при изменении координат внутри покоящейся жидкости для общего случая относительного покоя.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 777; Нарушение авторских прав?; Мы поможем в написании вашей работы!