
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Эквивалентность функций
|
|
|
|
По таблицам 2 и 3 легко заметить, что некоторые функции никак не зависят от значений некоторых своих аргументов. Так, например, функции g 1, g 4, f 1, f 16 не зависят от значений любого из аргументов, это константы ноль и единица. Функции f 4 и f 13 не зависят от значений аргумента у, а функции f 6 и f 11 – не зависят от аргумента х. Это позволяет выразить их как функции меньшего числа аргументов путем удаления аргумента, не влияющего на значения функции. Такой аргумент называют несущественной переменной для функции.
В противовес несущественным переменным, аргументы, от значений которых существенно зависят значения функции, называются существенными переменными. Таким образом, если переменная xi является существенной для функции f (x 1, x 2,…, xn), то обязательно существует такой набор значений остальных переменных a 1, a 2,…, ai -1, ai+ 1, ai+2,…, an, что значение функции при xi =1 не равно значению функции при xi =0, т.е. 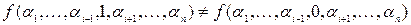 . Для несущественной переменной такого набора не существует.
. Для несущественной переменной такого набора не существует.
Две функции f 1 и f 2 называются эквивалентными или равными (обозначается это традиционно f 1 = f 2), если одна может быть получена из другой путем удаления или введения несущественной переменной.
Процедура удаления несущественной переменной xi на практике заключается в удалении всех строк вида: a 1, a 2,…, ai -1, 1, ai+ 1,…, an (т.е. таких строк, где переменная xi равна 1) и столбца xi из таблицы истинности функции. Введение несущественной переменной – обратный процесс.
Пример: пусть функция f (x, y, z) задана следующей таблицей истинности:
Таблица 4
| x | y | z | f (x, y, z) | |
| ¨ | ||||
| ¨ | ||||
| ¨ | ||||
| ¨ |
Из таблицы 4 видно, что значения функции не зависят от значений переменной у, поскольку на всех фиксированных наборах значений для x и z: (0,0), (0,1), (1,0) и (1,1), – значения функции при у =0 и у= 1 одинаковы. Тем самым, у – несущественная переменная, и её можно удалить. Для этого вычеркнем из таблицы 4 все помеченные строки, где у =1, и столбец у. Оставшиеся строки и столбцы таблицы будут определять функцию от двух переменных: х и z. Оформим результат в виде новой таблицы 5. Эта таблица является таблицей истинности элементарной функции. Это импликация. Итак, исходная функция эквивалентна импликации.
Таблица 5
| x | z | f (x, z) |
Рассмотрим теперь процедуру включения несущественной переменной. Для этого в таблицу 5 добавим новый столбец у, расположив его между столбцами х и z, и 4 новых строки: две в середине и две в конце таблицы. Скопируем значения переменных х и z, а также значения функции из двух верхних строк в добавленные ниже них, и из двух следующих строк в последние две. Заполним значения в столбце у так, чтобы в старых строках оно было равно 0, а в добавленных – 1. Получим таблицу истинности эквивалентной функции от большего числа переменных, совпадающую с таблицей 4.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 650; Нарушение авторских прав?; Мы поможем в написании вашей работы!