Реализация функций формулами

Классическое определение формулы алгебры логики вводится по шагам:

1) любая пропозициональная переменная является формулой;

2) если А формула, то выражение 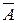или 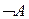тоже формула;

3) если А и В – формулы, то выражения вида (А & В), (А Ú В), (А ® В), (А º В) и прочие, где между А и В стоит пропозициональная связка, отличная от отрицания, – тоже формулы;

4) ничто иное не является формулой.

Формулы из пункта 1 называют элементарными. Формулы А и В из пунктов 2 и 3, если они не элементарны, называют подформулами составных формул.

При записи формул используются скобки для выделения подформул и указания порядка логических операций. В некоторых случаях скобки могут опускаться, это упрощает запись, делает её компактней. О соглашениях о бесскобочной записи формул будет сказано ниже.

Примеры формул:

1)

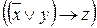
2)

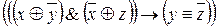
3)

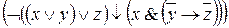
4) выражение вида 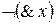формулой не является.

Итак, как следует из определения и примеров, формулы строятся из пропозициональных переменных, элементарных функций и скобок. Поэтому, когда необходимо подчеркнуть, что в построении формулы U участвуют переменные х ₁, х ₂,…, х_n, пишут: U (х ₁, х ₂,…, х_n). А в случае, когда надо указать, из каких элементарных функций построена формула, используется запись: U [ f ₁, f ₂,…, f_s ], где f ₁, f ₂,…, f_s – элементарные функции, встречающиеся в формуле.

Вычисление значений формулы выполняется путем подстановки различных наборов значений переменных, входящих в формулу. Результаты вычислений обычно оформляются в виде таблицы истинности формулы. Такие таблицы могут быть полными и сокращенными.

Для построения полной таблицы истинности исходную формулу разделяют на подформулы и затем вычисляют значение каждой подформулы. Таким образом, если n – это число переменных в формуле, а s – число выделенных подформул, то число столбцов в полной таблице истинности исходной формулы будет равно n + s, а число строк – 2 ⁿ. При этом последний столбец этой таблицы будет представлять значения формулы.

Для примера рассмотрим построение полной таблицы истинности формулы 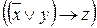. Разделим её на подформулы: f ₁=Ø x, f ₂= f ₁Ú y, f ₃= f ₂® z. Тем самым, таблица будет содержать 8 строк и 6 столбцов. См. таблицу 6.

Таблица 6

x	y	z	f 1	f 2	f 3

В последнем столбце таблицы 6 находятся значения исходной формулы.

Сокращенная таблица истинности строится непосредственно под формулой. Для этого выписывают саму формулу, затем под именами переменных записывают столбцы их значений, а под каждой логической связкой – столбец результатов соответствующей логической операции.

Рассмотрим построение сокращенной таблицы истинности на примере той же формулы: 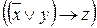. См. таблицу 7.

Таблица 7

((Ø	x	Ú	y)	®	z)
0

Внизу таблицы стрелками указаны участвующие в операции столбцы, номером в кружочке отмечен порядок выполняемых действий. Столбец результатов отмечен номером 3. Нетрудно заметить, что он совпадает с последним столбцом таблицы 6, но этого и следовало ожидать, поскольку способ оформления вычислений не должен оказывать влияния на результаты.

Из рассмотренных примеров видно также, что значениями формулы могут быть только 0 или 1. Поэтому столбец результатов можно рассматривать, как некоторую истинностную функцию, принимающую те же значения, что и формула, на соответствующих «энках». Эта функция соответствует формуле или, как говорят, реализуется формулой, про формулу в этом случае говорят, что она реализует функцию.

Пусть функция f (х ₁, х ₂,…, х_n) реализуется формулой U (х ₁, х ₂,…, х_n). Т.к. функция f может иметь несущественные переменные, то справедливо считать, что формула U реализует любую функцию, эквивалентную f. Если x_i – несущественная переменная для функции f, то функцию f можно заменить функцией g путем удаления несущественной переменной. Тогда формула U¹, полученная из формулы U отождествлением x_i с любой из оставшихся переменных, будет реализовывать функцию g.

Для подтверждения этого факта рассмотрим формулу: 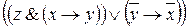. Вычислим значения этой формулы. См. таблицу 8.

Таблица 8

((z	&	(x	®	y)	Ú	(Ø y	®	Ø x))
1

Результат находится в столбце, отмеченном номером 4. Реализуемая формулой функция приведена в таблице 9. Эта функция имеет несущественную переменную z. Удалив эту переменную, получим функцию g (x, y), см. таблицу 10.

Таблица 9

x	y	z	f (x, y, z)

Таблица 10

x	y	g (x, y)

Далее отождествим в исходной формуле переменную z с переменной у. При этом будет получена новая формула: 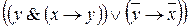. Построим таблицу истинности этой формулы. См. таблицу 11.

Таблица 11

((у	&	(x	®	y)	Ú	(Ø y	®	Ø x))
1

И, как видно из таблицы 11, новая формула реализует функцию g (x, y).

Если функция f ÎP₂ реализуется формулой U [ f ₁, f ₂,…, f_s ], сконструированной из функций f ₁, f ₂,…, f_s ÎP₂, то функция f называется суперпозицией функций f ₁, f ₂,…, f_s или говорят, что функция f получена с помощью операции суперпозиции из функций f ₁, f ₂,…, f_s.

Дата добавления: 2014-01-07