Тема 3. Решение игр в смешанных стратегиях. Величина называется ценой игры

Величина называется ценой игры.

Признак устойчивости (равновесности) пары стратегии - это равенство нижней и верхней цены игры. Про саму игру в этом случае говорят, что она решается в чистых стратегиях.

Если n >0, то игра выгодна для игрока А, если n <0 - для игрока В; при n =0 игра справедлива, т.е. является одинаково выгодной для обоих участников.

Если матрица игры содержит седловую точку, то ее решение сразу находится по принципу максимина.

Возникает вопрос: как найти решение игры, платежная матрица которой не имеет седловой точки? Применение максиминного принципа каждым из игроков обеспечивает игроку А выигрыш не менее a, игроку - проигрыш не больше b. Учитывая что a<b, естественно для игрока А желание увеличить выигрыш, а для игрока В - уменьшить проигрыш. Поиск такого решения приводит к необходимости применять смешанные стратегии: чередовать чистые стратегии с какими-то частотами.

Определение. Случайная величина, значениями которой являются чистые стратегии игрока, называется его смешанной стратегией.

Таким образом, задание смешанной стратегии игрока состоит в указании тех вероятностей, с которыми выбираются его чистые стратегии.

Будем обозначать смешанные стратегии игроков А и В соответственно

S_A=||p₁, p₂,..., p_m||,

S_B=||q₁, q₂,..., q_n||,

где p_i - вероятность применения игроком А чистой стратегии А _і;;

q_j - вероятность применения игроком В чистой стратегии B_j;.

В частном случае, когда все вероятности, кроме одной, равны нулю, а эта одна - единице, смешанная стратегия превращается в чистую.

Применение смешанных стратегий осуществляется, например, таким образом: игра повторяется много раз, но в каждой партии игрок применяет различные чистые стратегии с относительными частотами их применения, равными p _i и q _j.

Смешанные стратегии в теории игр представляют собой модель изменчивой, гибкой тактики, когда ни один из игроков не знает, какую чистую стратегию выберет противник в данной партии.

Если игрок А применяет смешанную стратегию S_A=||p₁, p₂,..., p_m||, а игрок В смешанную стратегию S_B=||q₁, q₂,..., q_n||, то средний выигрыш (математическое ожидание) игрока А определяется соотношением

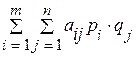. (2.6)

Естественно, что ожидаемый проигрыш игрока В равен такой же величине.

Дата добавления: 2014-01-07