Основные теоремы матричных игр

Итак, если матричная игра не имеет седловой точки, то игрок должен использовать оптимальную смешанную стратегию, которая обеспечит максимальный выигрыш n.

Естественно возникает вопрос: какими соображениями нужно руководствоваться при выборе смешанных стратегий? Оказывается принцип максимина сохраняет свое значение и в этом случае.

Если игрок А выбирает смешанную стратегию S_A=||p₁, p₂,..., p_m||, а игрок В смешанную стратегию S_B=||q₁, q₂,..., q_n||,то средний выигрыш математическое ожидание выигрыша игрока А (проигрыша игрока В) определится суммой

,

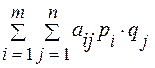которая может рассматриваться в качестве характеристики выбранных S_А и S_B.

Формируя свою стратегию S_А в антагонистической игре, игрок А в соответствии с принципом максимина должен выбрать такую стратегию, при которой минимально возможный выигрыш был бы максимален, т.е. такую стратегию, которая обеспечивает

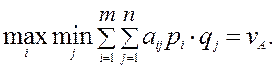(2.7)

Аналогичные рассуждения, связанные с поиском оптимальной смешанной стратегии игрока В, приводят к рекомендации выбрать такую стратегию S_B, которая обеспечивает

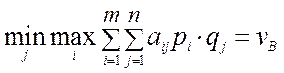. (2.8)

Весьма важным для теории и практики является вопрос о том, связаны ли между собой v _А и v _B. Ответ на него дает теорема о максимине.

Теорема о максимине. В конечной игре двух игроков (коалиций) с нулевой суммой (матричной игре) при 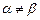имеет место равенство

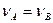. (2.9)

Теорема о максимине указывает на существование равновесия для случая v _А= v _B, при 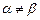и, следовательно, существования оптимальных смешанных стратегий.

Поэтому другая формулировка теоремы о максимине, называемая основной теоремой матричных игр определяется следующим образом.

Основная теорема матричных игр. Любая матричная игра имеет, по крайней мере, одно оптимальное решение, в общем случае, в смешанных стратегиях и соответствующую цену v.

Обе эти теоремы эквивалентны. Из этих теорем следует, что любая матричная игра имеет цену v. Цена игры v - средний выигрыш, приходящийся на одну партию, - всегда удовлетворяет условию

a£n£b, (2.10)

т.е. лежит между нижней a и верхней b ценами игры.

Оптимальное решение игры в смешанных стратегиях, также как и решение в чистых стратегиях, обладает тем свойством, что каждый из игроков не заинтересован в отходе от своей оптимальной смешанной стратегии, если его противник применяет свою оптимальную смешанную стратегию, так как это ему невыгодно.

Эта пара стратегий образует в игре положение равновесия: один игрок хочет обратить выигрыш в максимум, другой - в минимум, каждый “тянет” в свою сторону и, при оптимальном поведение обоих, устанавливается равновесие и устойчивый выигрыш n.

Определение. Те из чистых стратегий игроков А и В, которые входят в их оптимальные смешанные стратегии с вероятностями, не равными нулю, называются активными стратегиями.

Существует теорема об активных стратегиях, применение которой позволяет упрощать решение некоторых матричных игр.

Теорема об активных стратегиях. Если один из участников матричной игры G (m x n), придерживается своей оптимальной смешанной стратегии, то это обеспечивает ему максимальный средний выигрыш, равный цене игры n, независимо от того, какие действия предпринимает другой игрок, если только он не выходит за пределы своих активных стратегий

Решение матричной игры (2х2)

Пусть матричная игра G (2x2) имеет платежную матрицу

Bj   Ai	B1	B2
A1	a11	a12
A2	a21	a22

Предположим, что игра не имеет седловой точки, т.е. a¹b. При наличии седловой точки решение очевидно.

В соответствии с основной теоремой игра имеет оптимальное решение в смешанных стратегиях: S_A=||p₁, p₂|| и S_B=||q₁, q₂||, где вероятности применения (относительные частоты применения) чистых стратегий удовлетворяют соотношениям

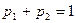; (2.11)

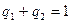. (2.12)

В соответствии с теоремой об активных стратегиях, оптимальная смешанная стратегия обладает тем свойством, что обеспечивает игроку максимальный средний выигрыш, равный цене игры n, независимо от того, какие действия предпринимает другой игрок, если тот не выходит за пределы своих активных стратегий. В частности, если игрок А использует свою оптимальную смешанную стратегию, а игрок В - свою чистую активную стратегию В₁, то цена игры n равна

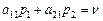, (2.13)

а при использовании игроком В чистой активной стратегии В ₂, выигрыш будет равен

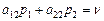. (2.14)

Уравнения (2.11), (2.13) и (2.14) образуют систему трех линейных алгебраических уравнений с тремя неизвестным:

р₁, р₂ и n.

Решая ее, легко находим, что

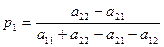. (2.15)

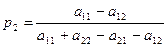. (2.16)

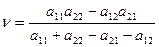. (2.17)

Если игрок В использует свою оптимальную смешанную стартегию, а игрок А - свою чистую активную стратегию А₁, то цена игры n равна

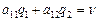, (2.18)

а при использовании игроком А чистой активной стратегии А₂, выигрыш будет равен

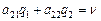. (2.19)

Уравнения (2.12), (2.18) и (2.19) образует систему трех линейных алгебраических уравнений с тремя неизвестными: q₁; q₂ и n.

Решая ее, легко находим, что

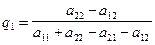. (2.20)

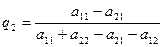. (2.21)

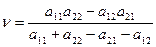. (2.22)

Естественно, что в обоих случаях цена игры (выражения (2.17) и (2.22)) получилась одна и та же.

Чтобы соотношения (2.15), (2.16), (2.17), (2.20), (2.21), (2.22) имели смысл, необходимо потребовать, чтобы

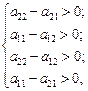
или

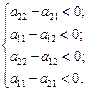
Тогда 0<p₁<1; 0<p₂<1; 0<q₁<1; 0<q₂<1.

Нетрудно заметить, что в этих неравенствах отражено предположение об отсутствии в рассматриваемой игре седловой точки. Действительно, ни один из четырех выигрышей а₁₁, а₁₂, а₂₁, а₂₂ не может удовлетворить этим неравенствам, будучи минимальным в своей строке и максимальным в своем столбце.

Решения системы уравнений (2.15), (2.16), (2.17) и (2.20), (2.21), (2.22), полученные алгебраическим методом, удобно получать и графическим методом (рис. 2.4). Для нахождения вероятностей р ₁, р ₂ и цены игры v в прямоугольной системе координат по оси абсцисс откладывается вероятность р ₁Î[0,1], а по оси ординат - соответствующие этой вероятности - выигрыши игрока А.

При р₁=0, игрок А применяет чистую стратегию А ₂. Если при этом игрок В применяет чистую стратегию В ₁, то выигрыш игрока А равен а₂₁ (уравнение (2.13)), а если игрок В применяет чистую стратегию В ₂, то выигрыш игрока А равен а₂₂ (уравнение (2.14)). При р₁=1, игрок А применяет чистую стратегию А ₁.

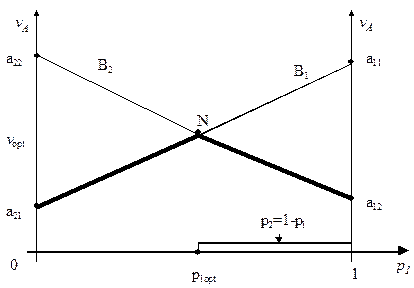
Рис. 2.4

Если при этом игрок В применяет чистую стратегию В ₁, то выигрыш игрока А равен а₁₁, а при применении чистой стратегии В₂ - а₁₂. Так как значения р₁ лежат в пределах [0,1], то соединяя крайние точки для стратегий В₁ и В₂ (строя графики функций v_А =(a₁₁-a₂₁)p₁+a₂₂ и v_А =(a₁₂-a₂₂)p₁+a₂₂), получаем значения выигрышей игрока А для всех промежуточных значений р ₁.

В соответствии с принципом максимина, игрок А должен выбрать такую смешанную стратегию, при которой его минимальный выигрыш максимален. Точка N пересечения отрезков прямых (рис. 2.4) и определяет как оптимальную цену игры v _opt, так и оптимальные вероятности p _1opt и p _2opt=1- p _1opt, соответствующие оптимальной смешанной стратегии игрока А, т.е. дает решения системы уравнений (2.11), (2.13), (2.14).

Для графического решения системы уравнений (2.12), (2.18), (2.19) отложим по оси абсцисс вероятность q₁Î[0,1], а по оси ординат соответствующие этой вероятности выигрыши игрока В:

v_В =(a₁₁-a₁₂)q₁+a₁₂; (2.23)

v_В =(a₂₁-a₂₂)q₁+a₂₂. (2.24)

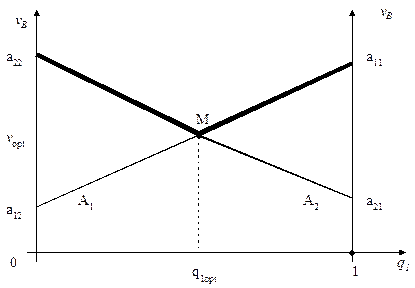
Рис. 2.5

Решением являются координат точки М пересечения прямых, описываемых уравнений (2.23) и (2.24):

q_1opt;q_2opt=1-q_1opt и v _opt.

Это же следует и из принципа максимина, в соответствии с которым игрок В должен выбрать такую смешанную стратегию, при которой его максимальный проигрыш будет минимальным.

Пример: Найти алгебраическим и геометрическим методами решение игры, платежная матрица которой имеет вид

Bj   Ai	B1	B2	a i
A1		-2	-2
A2
b j

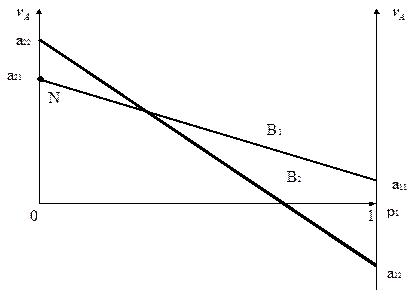
Рис. 2.7

В данной игре нижняя цена игры a=1 не равна верхней цены игры b=3, поэтому игра не имеет седловой точки и, в соответствии с основной теоремой матричных игр, имеет оптимальное решение в смешанных стратегиях.

Для игрока А, в соответствии с формулами (2.15) и (2.16), оптимальные вероятности применения стратегий А₁ и А₂ равны:

;

.

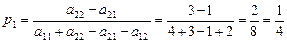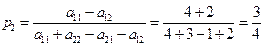Для игрока В, в соответствии с формулами (2.20) и (2.21), оптимальные вероятности применения стратегий В₁ и В₂ равны:

;

.

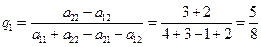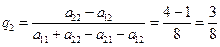Таким образом, оптимальные смешанные стратегии игроков 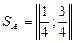; , а цена игры в соответствии с формулой (2.22) равна:

.

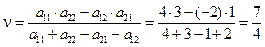Так как n >0, то игра выгодна для игрока А.

Графическое изображение игры для игрока А показана на рис. 2.8.

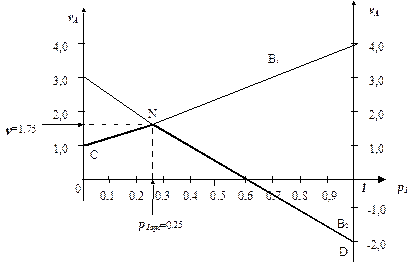
Рис. 2.8

Нижняя граница выигрыша игрока А определяется ломаной CND. Оптимальное решение, определяется точкой N, естественно, дает тоже решение, что и алгебраический метод: .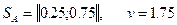

Геометрическое изображение игры для игрока В показано на рис.2.9.

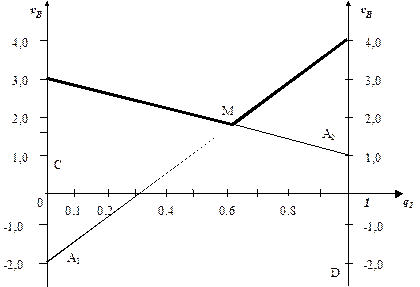
Рис. 2.9

Оптимальное решение, определяемое точкой М, дает решение .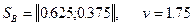

Дата добавления: 2014-01-07