Решение игр mхn. Эквивалентные задачи линейного программирования

Пусть имеется матричная игра mxn без седловой точки с матрицей выигрышей ||a_ij||. Допустим, что все выигрыши a_ijположительны (этого всегда можно добиться, прибавляя ко всем элементам матрицы достаточно большое число С; от этого, как уже отмечалось, цена игры увеличится на C, а оптимальные решения S_Aи S_Bне изменятся).

Если все aij положительны, то и цена игры при оптимальной стратегии тоже положительна, т.к. .

В соответствии с основной теоремой матричных игр, если платежная матрица не имеет седловой точки, то имеется пара оптимальных смешанных стратегий S_A=||p₁, p₂,..., p_m|| и S_B=||q₁, q₂,..., q_n||, применение которой обеспечивает игрокам получение цены игры .

Найдем вначале S_A. Для этого предположим, что игрок В отказался от своей оптимальной смешанной стратегии S_Bи применяет только чистые стратегии. В каждом из этих случаев выигрыш игрока А будет не меньше, чем :

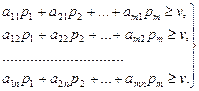(2.25)

Разделив левую и правую часть каждого из неравенств (2.25) на положительную величину v и введя обозначения:

(2.26)

запишем неравенства (2.25) в следующем виде:

, (2.27)

где x₁, x₂,... x_m- неотрицательные переменные.

В силу того, что

p₁+p₂+...+p_m=1,

переменные x₁, x₂,... x_mудовлетворяют условию

. (2.28)

Учитывая, что игрок А стремится максимизировать , получаем следующую задачу линейного программирования: найти неотрицательные значения переменных x₁, x₂,... x_mтакие, чтобы они удовлетворяли линейным ограничениям - неравенствам (2.27) и обращали в минимум линейную функцию этих переменных:

min L (x)=x₁+x₂+... +x_m. (2.29)

Из решения задачи линейного программирования находим цену игры и оптимальную стратегию Saпо формулам:

, (2.30)

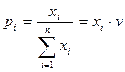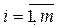, . (2.31)

Аналогично находим оптимальную стратегию S_Вигрока В. Предположим, что игрок А отказался от своей оптимальной стратегии S_Aи применяет только чистые стратегии. Тогда проигрыш игрока В в каждом из этих случаев будет не больше, чем :

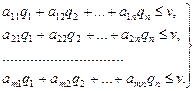. (2.32)

Разделив левую и правую части каждого их неравенств (2.32) на положительную величину и введя обозначения:

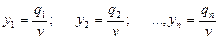, (2.33)

запишем неравенство (2.32) в следующем виде:

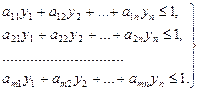, (2.34)

где y₁, y₂,..., y_n- неотрицательные переменные.

В силу того, что q₁+q₂+...+q_n=1, переменные y₁, y₂,..., y_nудовлетворяют условию

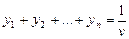. (2.35)

Учитывая, что игрок В стремится минимизировать положительную цену v (свой проигрыш), получаем задачу линейного программирования: найти неотрицательные значения переменных y₁, y₂,..., y_nтакие, чтобы они удовлетворяли линейным ограничениям (2.34) и обращали в максимум линейную функцию этих переменных:

max L (y)=y₁+y₂+... +y_m. (2.36)

Эта задача является двойственной по отношению к задаче, представленной условиями (2.27) и (2.29).

Оптимальная стратегия S_B=||q₁, q₂,..., q_n|| игрока В определяется из решения двойственной задачи линейного программирования по формулам:

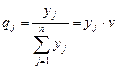, . (2.37)

Таким образом, оптимальные стратегии S_A=||p₁, p₂,..., p_m|| и S_B=||q₁, q₂,..., q_n|| матричной игры mxn с платежной матрицей ||a_ij|| могут быть найдены путем решения пары двойственных задач линейного программирования:

Прямая (исходная) задача	Двойственная задача
, , ; , .	, , ; , .

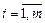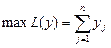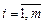При этом

, (2.38)

.

Пример. Найти решение и цену матричной игры, платежная матрица которой имеет вид

Bj   Ai	B1	B2	B3
A1
A2
A3

Дата добавления: 2014-01-07