Теоретический анализ контактных напряжений при осадке

Для описания силовой картины процесса осадки примем гипотезу плоских сечений. Согласно этой гипотезе, можно считать деформации неизменными во всех слоях по высоте образца. Следовательно, зоны скольжения, торможения и застоя также простираются по всей высоте. Напряжения по высоте имеют постоянные значения, равные контактным. Выход бокового металла на контактную площадку отсутствует, и ширина увеличивается во времени одинаково по всей высоте образца. Как видно, гипотеза плоских сечений грубо искажает картину деформации образца и применима весьма приближённо для описания деформированного состояния металла. Однако при правильном задании сил трения на контакте это не сказывается на расчетах давления металла на бойки, поскольку давление полностью определяется силами трения (то есть функция трения выступает здесь в качестве подгоночной). Конечно, речь идет только о средних и низких очагах деформации, так как при высоких, наоборот, все, в том числе силовые параметры, определяются характером распределения деформации по объему. На высоких очагах гипотеза плоских сечений неприменима даже для описания силовой картины.

Рассмотрим в такой постановке задачу об осадке параллелепипеда, имеющего высоту h, ширину b и очень большую длину l. При большой длине можно выделить среднюю часть образца и считать, что в этой части в направлении длины деформации равны нулю, металл находится в условиях плоской деформации. Для описания напряжений достаточно рассмотреть одно сечение образца с размерами h и b.

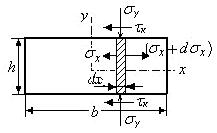
Рис. 35. К равновесию сил при осадке

Выделим элемент l´h´ dx (рис 35) толщиной dx и спроектируем на ось х все силы, действующие на этот элемент. Получим

- дифференциальное уравнение равновесия горизонтальных сил (длина образца сокращается):

После преобразований оно запишется в виде:

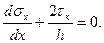
Для поиска неизвестных добавим к этому уравнению

- условие начала пластического течения

,

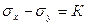- и условие трения на контактных поверхностях

.

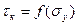Продифференцируем условие пластичности (считаем К =const), получим

.

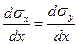Подставим это выражение в уравнение равновесия и получим

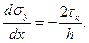
Рассмотрим полученную систему из трёх уравнений (включая последнее) отдельно для зон скольжения, торможения и застоя, в которых условия трения различаются.

Дата добавления: 2014-01-07