Минимизация абстрактного автомата Мура

Минимизация автоматов Мура основана на тех же принципах, что и минимизация автоматов Мили. Для табличного описания эта процедура алгоритмизирована и состоит из трёх шагов.

Шаг 1 Распространение неопределённости выходов на таблицу переходов. Если в автомате Мура для некоторого состояния выходной сигнал не определён, то в это состояние он не может попасть под действием допустимого входного слова. Переход в таблице, соответствующий этому состоянию, исключается, а в остальных клетках таблицы переход в исключённое состояние заменяется специальным символом, например, прочерком.

Шаг 2 Исключение недостижимых состояний. Если нет ни одного слова, приводящего автомат в состояние a_i, отличающееся от начального, то такое состояние исключается вместе с соответствующими переходами таблицы переходов.

Пример выполнения двух начальных этапов минимизации автомата Мура S₁₄ приведён в таблице 35 и таблице 36.

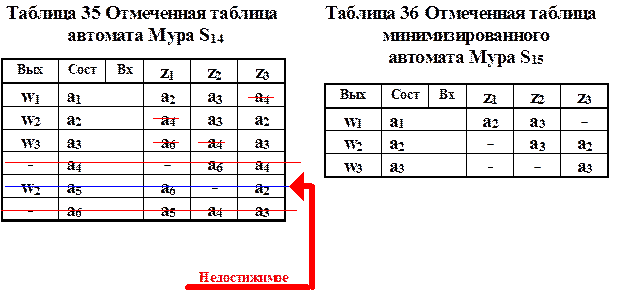
Шаг 3 Нахождение совместимых состояний автомата Мура. Состояния автомата Мура являются 0-совместимыми, если, не считая неопределённых отметок, они отмечены одинаковыми выходными сигналами. Состояния являются i - совместимыми для любого i = 1;2;..., если они 0-совместимы и автомат, переходя из них, перерабатывает допустимые слова длиной i одинаково. Процедура расщепления классов обязательно закончится за ограниченное количество шагов и, следовательно, более нерасщепляющиеся классы образуют конечные классы совместимых состояний. После нахождения совместимых состояний автомата строится минимизированный нормализованный автомат Мура.

При табличном описании нормализованного автомата Мура, имеющего N_n классов совместимых состояний, переход d(N_i, z_j) считается неопределённым, если для всех a_i Î N_i переходы d(a_i, z_j) неопределённы. Если хотя бы для одного a_i Î N_i переход d(a_i, z_j) определён, то в таблице нормализованного автомата указывается именно этот класс N_k, в который происходит переход. У частичного автомата таких переходов возможно несколько. Каждое класс N_i отмечается выходным сигналом который соответствует всем состояниям этого класса.

Построенный таким образом нормализованный автомат является минимальным, если исходный автомат был полностью определённым. Если исходный автомат был частичным, то возможно, либо доопределение нормализованного автомата в процессе нахождения совместимых состояний, либо получение частичного нормализованного автомата. Доопределение и выбор минимального автомата для частичного нормализованного автомата выполняется путем перебора и оценки всех вариантов автоматов, построенных по описанию нормализованного автомата.

Более подробно рассмотрим применение методики минимизации автоматов Мура на примере полностью определённого автомата S₁₆.

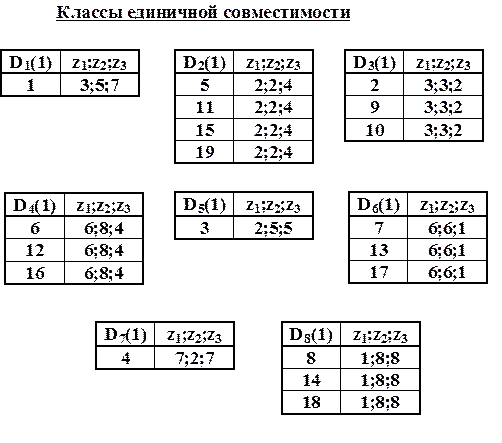
Дата добавления: 2014-01-07