Решение. 1. Задаем направление возможного движения при достижении условия предельного равновесия

1. Задаем направление возможного движения при достижении условия предельного равновесия. Пусть за счет достаточно большой, по
сравнению с моментом М, силы F произойдет движение системы влево. Тогда момент трения качения, приложенный к цилиндру 2, будет направлен по часовой стрелке (рис. 11.2.7). Его величину находим
по формуле М_тр = N ₂ ∙ f_к.

2. Решаем задачу о равновесии системы двух цилиндров и стержня.
Разбиваем систему на три тела (рис. 11.2.6, 11.2.7, 11.2.8). Внешние связи за­
меняем реакциями F _сц1, N ₁, F _сц2, N ₂.

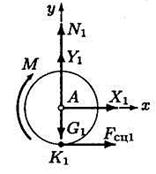
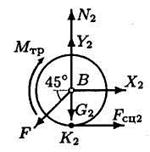
Рис. 11.2.6 Рис. 11.2.7 Рис. 11.2.8

Реакции F _сц1 и F _сц2 приложены к цилиндрам в точках их касания поверхностей, вызваны силами сцепления (трения) и обеспечивают вращение цилиндров. Реакции внутренних связей — Х ₁, Y ₁, Х ₂, Y ₂.

При составлении системы семи уравнений с неизвестными Х ₁, Y ₁, N ₁, X ₂, Y ₂, N ₂, M избегаем уравнения, в которые входят неизвестные реакции F _сц1 и F _сц2.

Составляем уравнения равновесия для цилиндра 1 (рис. 11.2.6):

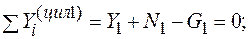
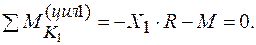(1)

Уравнения равновесия цилиндра 2 (рис. 11.2.7) имеют вид

(2)

Уравнения равновесия стержня АВ (рис. 11.2.8) имеют вид

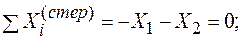
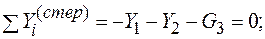
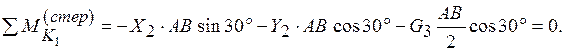(3)

Из решения системы уравнений (1-3) определяем:

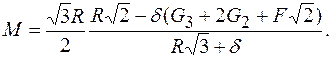(4)

Радиус и коэффициент трения качения переводим в метры R = 0.5 м, f_к = 0.002 м. Получаем М = 3.414 Нм. Вычисляем нормальные реакции опор:

N ₁ = 36.058 Н, N ₂ = 61.013 Н.

Убеждаемся, что N ₁ > 0 и N ₂ > 0, что соответствует наличию опоры. Если реакция опоры равна нулю, то это означает отрыв тела от по­верхности, отрицательной реакции опоры N ≤ 0 в задаче с односто­ронней связью не существует (физически не реализуется).

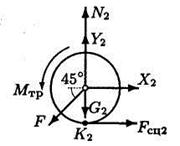
Рис. 11.2.9

3. Меняем направление возможного движения системы. Пусть за счет действия момента М произойдет движение системы вправо. Мо­мент трения качения направим против часовой стрелки (рис. 11.2.9). Составляя уравнения равновесия для новой системы сил, заметим, что отличие от прежней системы про­является только в знаке М во вто­ром уравнении равновесия (2). Так как М_тр = N ₂∙8, то новое решение для М будет формально отличаться от (4) только знаком у коэффициента трения f_к. Поэтому, не решая (и даже не со­ставляя) системы уравнений равнове­сия типа (1— 3) для нового направления возможного движения, записываем ответ, изменяя знаки у f_к в (4):

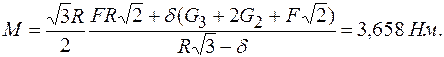(5)

Точно так же находим нормальные реакции опор: N ₁ = 35.776 Н, N ₂ = 61.295 Н. При равновесии системы момент, приложенный к цилиндру 1, изменяется в пределах (в Нм) (В задачах, где допускается проскальзывание, необходимо находить также силы F _cц1 и F _cц2 и проверять условие проскальзывания F _cц1 = F _тp1 < fN ₁, F _cц2 = F _тp2 < fN ₂, где f — коэффициент трения скольжения).

3.414 ≤ М ≤ 3.658.

Дата добавления: 2014-01-07