Устойчивость при опрокидывании

Рычагом называется твердое тело, имеющее неподвижную ось вра­щения и находящееся под действием сил, лежащих в плоскости, перпен­дикулярной этой оси. Положим, что к рычагу в точках 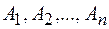приложены зада­ваемые силы 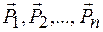, лежащие в плоскости чертежа, а ось рычага пересекает эту плоскость в точке О, которую называют опорной точкой (рис. 6.10).

Реакция 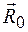оси рычага, урав­новешивая задаваемые силы, ле­житв их плоскости, но направ­ление ее не известно.

Разложим реакцию оси рычага на две составляющие 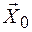и 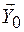и составим три уравнения равнове­сия сил, действующих на рычаг:

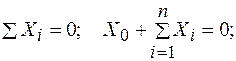(6.8)

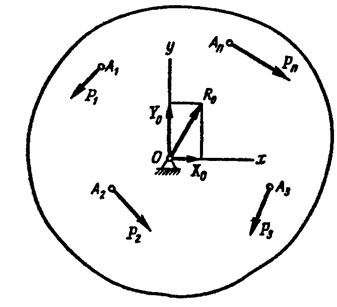
Рис. 6.10

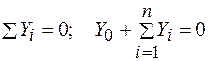; (6.9)

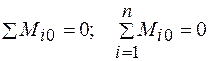. (6.10)

Здесь - суммы проекций задаваемых сил, приложенных к рычагу на оси х и у; Х₀ и Y₀ - проекции реакции оси рычага на оси; - сумма моментов задаваемых сил относительно опорной точки.

Уравнение (6.10), не содержащее реакции оси рычага, выражает условие, которому удовлетворяют задаваемые силы, приложенные к рычагу, если он находится в покое.

Это условие формулируется так: если рычаг находится в покое, то алгебраическая сумма моментов всех задаваемых сил, приложенных к рычагу, относительно опорной точки равна нулю:

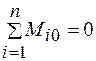. (6.11)

Из уравнений (6.11) и (6.9) равновесия определяются модуль и направле­ние реакции оси рычага. Из условия (6.11), которое выполняется, если рычаг находится в покое, получим условие устойчивости тел при опро­кидывании.

Положим, что к прямоугольному параллелепипеду (рис. 6.11) весом 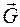на высоте d приложена горизонтальная сила 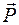, которая может не только сдвинуть тело, но и опрокинуть его при вращении вокруг ребра А. Считая, что сила 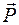недостаточно велика, чтобы сдвинуть тело, рассмотрим ее опрокидывающее действие. Обозначим а расстояние от точки А, изображающей на рисунке 6.12 ось вращения рычага, до линии действия силы 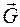, которая препятствует опрокидыванию.

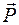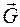Составим сумму моментов задаваемых сил и относительно опорной точки А:

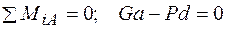, откуда .

Назовем абсолютные значения моментов сил 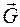и 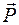относительно точки А удерживающим и опрокидывающим моментами:

.

Тогда на границе устойчивости

.

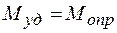При устойчивом состоянии тела

.

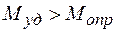Устойчивость при опрокидывании в технике принято определять отношением числового значения удерживающего момента к числовому значению опрокидывающего момента:

.

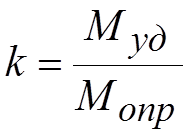Это отношение называют коэффициентом устойчивости. Очевидно, что в случае предельной устойчивости коэффициент устойчивости k = 1, а в случае устойчивого состояния k > 1.

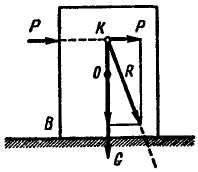
Рис. 6.11 Рис. 6.12

Определить, опрокинется ли тело под действием силыили будет нахо­диться в устойчивом состоянии, можно и графическим путем. Для этого продолжим линии действия сил 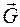и 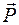до их пересечения в точке К, перенесем силы в эту точку и найдем их равнодействующую (рис. 6.12).

Продолжая линию действия равнодействующей силы, найдем точку ее пересечения с опорной плоскостью.

В рассмотренном примере возможны три случая:

1. Если эта точка лежит слева от ребра А, то состояние тела устой­чиво.

2. Если линия действия равнодействующей пересекает ребро А, тосостояние тела предельно устойчиво.

3. Если эта точка лежит справа от ребра А, то тело опрокинется.

Задача 6. Определить вес противовеса G ₁, обеспечивающий коэффициент устойчивости нагруженного крана при опрокидывании, равный 1,5, если вес крана G ₂=50 кН, вес груза G ₃=40 кН. Размеры указаны на рис. 6.13.

Рисунок 6.13

Решение. Предполагаемое опрокидывание крана под действием веса груза является вращением вокруг оси О, совпадающей с правым рельсом. Силами, препятствующими опрокидыванию, являются вес крана и вес про­тивовеса 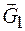. Определим опрокидывающий момент как абсолютное значение момента силы 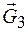относительно точки О:

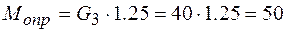кНм.

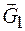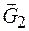Определим удерживающий момент как сумму абсолютных значений момен­тов сил и относительно точки О:

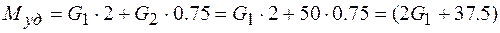кНм.

Воспользуемся коэффициентом устойчивости тела при опрокидывании

.

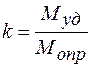Отсюда

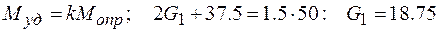кН.

Трибоника— раздел механики, в котором изучаются основы трения, смазки, износа и влияние этих процессов на структуру и функцию динамических механических систем. Так как трение определяет основные потери полезной механической энергии, а износ является главной причиной замены оборудования, углубленное понимание и эффективное применение основ трибоники жизненно важны для сохранения энергии и материалов в технической конструкции.

Дата добавления: 2014-01-07