
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Умножение матриц
|
|
|
|
1) Не любые две матрицы можно перемножить.
2) Для того, чтобы два матрицы А и В можно было перемножить, число столбцов матрицы А должно быть равно числу строк матрицы В.
Пусть матрица 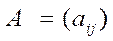 размерности m
размерности m 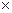 n и матрица
n и матрица  размерности n
размерности n 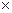 k. Тогда матрица
k. Тогда матрица – размерности m
– размерности m 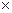 k определяется следующим образом.
k определяется следующим образом.
Определение: Произведением матрицы  ) на матрицу
) на матрицу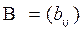 называется матрица
называется матрица  элементы
элементы которой представляют собой сумму произведений элементов i -той строки матрицы А на элементы j -того столбца матрицы В. Обозначается С = А
которой представляют собой сумму произведений элементов i -той строки матрицы А на элементы j -того столбца матрицы В. Обозначается С = А 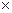 В.
В.
Возьмем, например, матрицы второго порядка
А =  , В =
, В =  .
.
Тогда
А 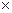 В =
В = 
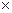
 =
=  .
.
Пример:
А =  ; В =
; В = 
А2*3 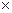 В3*1 = С2*1
В3*1 = С2*1
С =  .
.
Свойства умножения матриц:
1. Умножение матриц некоммутативно: А 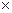 В ≠ В
В ≠ В 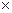 А.
А.
Пример:
А 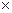 В =
В = 
В 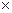 А =
А =  .
.
2. Умножение матриц ассоциативно:
А 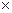 (В
(В 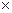 С) = (А
С) = (А 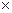 В)
В) 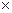 С
С
3. Умножение матриц дистрибутивно относительно сложения матриц:
А 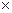 (В + С) = А
(В + С) = А 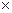 В + А
В + А 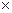 С
С
4. Для любой квадратной матрицы А
А 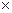 Е = Е
Е = Е 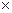 А = А.
А = А.
(Е-единичная матрица той же размерности, что и матрица А).
Определители второго и третьего порядка
Определение. Матрицей второго порядка называется таблица вида
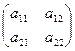
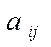 – числа– элементы матрицы,
– числа– элементы матрицы,
i – номер строки,
j – номер столбца.
Матрицы обозначается
 .
.
Определение. Определителем второго порядка называется число  .
.
Обозначается  .
.
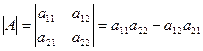 .
.
Пример. 1) 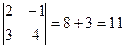 .
.
2) Решить уравнение:  .
.

Определение. Рассмотрим таблицу вида 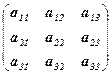 , где
, где
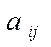 – числа – элементы матрицы,
– числа – элементы матрицы,
i - номер строки,
j - номер столбца.
Такая таблица называется матрицей третьего порядка.
Определение. Определителем третьего порядка называется число
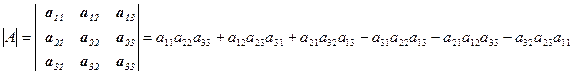 .
.
Пример.  .
.
Свойства определителей
1. Величина определителя не изменится, если строки и столбцы поменять местами.
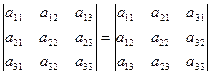
2. Если определитель содержит нулевую строку, то он равен нулю.
3. Если определитель содержит две одинаковые или пропорциональные строки, то он равен нулю.
4. Если переставить местами две строки, то определитель поменяет знак.
5. Если элементы строки умножить на k, то и определитель умножиться на k.
6. Определитель не измениться, если к элементам некоторой строки прибавить элементы другой строки, умноженные на одно и то же число.
Замечание. Свойства 2 – 6 справедливы и для столбцов (в силу свойства 1).
Решение систем линейных уравнений с помощью определителей.
Правило Крамера
Система двух линейных уравнений с двумя неизвестными имеет вид
 (1)
(1)
Здесь
x, y – неизвестные системы,
 - коэффициенты системы,
- коэффициенты системы,
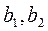 - свободные члены системы.
- свободные члены системы.
Решить систему (1) – это значит найти такие x и y, при подстановке которых уравнения преобразуются в тождества (верные равенства).
Составим определители:
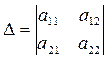 - определитель системы,
- определитель системы,
 ,
,  .
.
Возможны следующие случаи:
1. Если 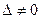 , то система (1) имеет единственное решение.
, то система (1) имеет единственное решение.
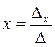 ;
;  (2)
(2)
(2) – Формулы Крамера.
2. Если  или
или 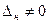 , то система несовместна (не имеет решений).
, то система несовместна (не имеет решений).
3. Если  , то система неопределена (имеет бесконечное множество решений).
, то система неопределена (имеет бесконечное множество решений).
Пример. 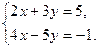
 ,
,
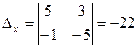 ,
, 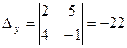 .
.
Система имеет единственное решение:
 ;
;  .
.
Ответ.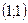 .
.
Рассмотрим систему трёх линейных уравнений с тремя неизвестными
 (3)
(3)
Составим определители:
 ,
, 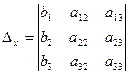 ,
,
 ,
,  .
.
Возможны случаи.
1. Определитель системы 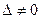 , тогда система имеет единственное решение.
, тогда система имеет единственное решение.
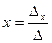 ,
,  ,
,  (4)
(4)
(4) – Формулы Крамера.
2. Если 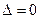 ,
,  или
или  , или
, или 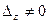 , то система несовместна (не имеет решений).
, то система несовместна (не имеет решений).
3. Если  , то система неопределенная (имеет бесконечное множество решений).
, то система неопределенная (имеет бесконечное множество решений).
Пример: 
Найдем определители.
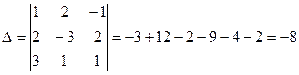 ,
,
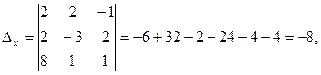
 ,
,
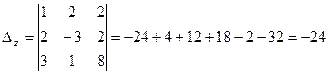 .
.
Найдем неизвестные по формулам (4).

Ответ. (1; 2; 3).
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 382; Нарушение авторских прав?; Мы поможем в написании вашей работы!