Элементы физики атома и атомного ядра

Вопросы, выносимые на СКР:

1. Тепловое излучение.
2. Фотоэффект. Его виды и законы.
3. Эффект Комптона.
4. Волны де Бройля.
5. Соотношение неопределенностей Гейзенберга.
6. Вынужденное излучение. Лазеры.
7. Эффект Мессбауэра.
8. Элементарные частицы.

§1. Атом водорода.

Атом – это наименьшая часть химического элемента, являющаяся носителем его свойств. Атом состоит из тяжелого ядра, обладающего положительным зарядом, и окружающих его легких частиц – электронов, обладающих отрицательным зарядом. Атом – нейтральное образование, поэтому заряд ядра равен суммарному заряду электронов.

В начале ХХ в. среди других моделей атома выделялась предложенная в 1911 г. Резерфордом ядерная (планетарная модель) атома, явившаяся важным шагом на пути к современным представлениям о строении атома. Согласно этой модели, вокруг положительного ядра с зарядом Ze (Z – порядковый номер элемента в системе Менделеева, е – элементарный заряд) по круговой (или эллиптической) орбите под действием сил электростатического притяжения движутся электроны. Заряд ядра равен суммарному заряду электронов, поскольку атомы нейтральны. При движении электрона вокруг ядра возникает орбитальный магнитный момент

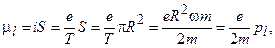(1.1)

где i – круговой ток, S – площадь орбиты, Т – период обращения по орбите, e и m – заряд и масса электрона соответственно, R – радиус орбиты, ω – угловая частота, р _l – орбитальный механический момент количества движения.

μ_l и р_l представляют собой векторы, направленные в противоположные стороны, поскольку заряд электрона отрицателен.

Из формулы (1) следует, что отношение магнитного момента к механическому, называемое гиромагнитным отношением

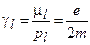(1.2)

есть величина постоянная, не зависящая от радиуса орбиты, по которой движется электрон.

Гиромагнитное отношение принято выражать в единицах e/2m и обозначать буквой g, тогда g_l=1.

Модель Резерфорда не позволяла объяснить многие экспериментально установленные факты, поэтому на смену ей пришла полуквантовая модель Н. Бора. В основу своей теории Бор положил два постулата.

Первый постулат Бора: в атоме существуют стационарные состояния, характеризующиеся определенными дискретными значениями энергии, в которых он не излучает энергии. Стационарным состояниям атома соответствуют стационарные орбиты, по которым движутся электроны. Движение электронов по стационарным орбитам не сопровождается излучением электромагнитных волн.

В стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь дискретные квантованные значения момента импульса, удовлетворяющие условию

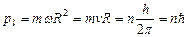(1.3)

где h – 6,65×10^-34 Дж×с, n – главное квантовое число, равное 1, 2, 3…, v – линейная скорость.

Сопоставление формул (1.1) и (1.3) показывает, что в модели Бора квантуется не только механический, но и магнитный момент, так как

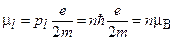(1.4)

где

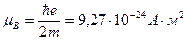(1.5)

- наименьшее значение орбитального магнитного момента, соответствующего движению по первой боровской орбите (n=1), называемое магнетоном бора.

Второй постулат Бора: при переходе атома из одного стационарного состояния в другое излучается (поглощается) фотон с энергией

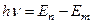. (1.6)

Равной разности энергий соответствующих стационарных состояний. При Е_m<E_n происходит излучение фотона, при Е_m>E_n – его поглощение. Набор возможных дискретных частот определяет линейчатый спектр атома.

Следуя Бору, рассмотрим движение электрона в атоме водорода, ограничиваясь для простоты круговыми стационарными орбитами. На основании второго закона Ньютона для электрона, движущегося под действием кулоновской силы,

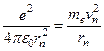(1.7)

Решив это предложенное Резерфордом равенство относительно r_n и подставив скорость v_n из условия квантования (1.3), получим выражение для радиуса n-й стационарной орбиты:

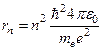(1, 2, 3 …) (1.8)

Выражение (1.8) задает радиусы разрешенных орбит в боровской модели атома водорода. Ближайшей к ядру орбите соответствует n=1, поэтому первый боровский радиус (а)

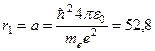пм (1.9)

и зависит лишь от фундаментальных постоянных. Из соотношения (1.8) следует, что r_n=n²r₁, т.е. радиусы орбит для стационарных состояний квантованы и равны соответственно r₁, 4r₁, 9r₁,....Каждый из этих радиусов пропорционален квадрату целого числа n, называемому квантовым числом.

Потенциальная энергия электрона в электростатическом поле ядра

.

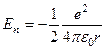Учитывая квантованные для радиусов стационарных орбит значения (1.8), получаем

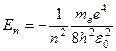(n=1, 2, 3,...), (1.10)

где знак минус означает, что электрон находится в связанном состоянии. Из выражения (1.10) следует, что энергия электрона в атоме водорода может принимать только дискретные значения, т.е. энергия атома квантуется. Поставив в (1.10) фундаментальные постоянные и выразив энергию в электрон-вольтах, получим, что

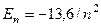эВ (1.11)

т.е. энергетические состояния атома водорода образуют последовательность энергетических уровней, изменяющихся в зависимости от n. Состояние с минимальной энергией, или основное состояние, соответствует n=1, а его энергия Е=-13,6 эВ. Состояния с n>1 является возбужденными.

Придавая n различные целочисленные значения, получаем для атома водорода, согласно формуле (1.11), возможные уровни энергии стационарных состояний электрона, схематически представленных на рис. 1.1 в виде горизонтальных прямых. С увеличением квантового числа n энергетические уровни все больше и больше сближаются и при n®¥ Е®0.

Электронам, связанным в атоме, отвечает Е<0. Для удаления электрона из атома, находящегося в основном состоянии, требуется затратить энергию, называемую энергией ионизации. Как следует из рис. 1.1, Е_i=13,6 эВ. Для удаления электрона из атома, следует затратить энергию, называемую энергией связи данного состояния. Так, например, энергия связи первого возбужденного состояния равна 3,4 эВ (рис. 1.1).

Согласно второму постулату Бора, при переходе атома водорода из стационарного состояния n в стационарное состояние m с меньшей энергией испускается фотон, энергия которого (с учетом 1.10)

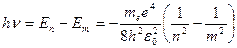(1.12)

Откуда частота излучения

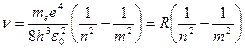(1.13)

где R=m_ee⁴/(8h³ε₀²) – величина, совпадающая с постоянной Ридберга в эмпирических формулах для атома водорода.

На рис. 1.1 стрелками показаны переходы, приводящие к излучению линий, принадлежащих к различным сериям спектра излучения атома водорода.

Основной недостаток теории Бора заключается в том, что она представляла собой компромиссное сочетание классической физики с квантовой теорией излучения. Методологически теория Бора требовала решения задач средствами классической физики с последующим отбором дискретных величин, удовлетворяющих требованиям квантовой механики. Выводы теории Бора оказались справедливыми лишь для самых простейших случаев.

§2. Элементы физики атомов и молекул.

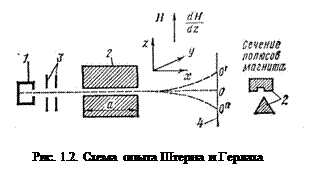Опыт Штерна и Герлаха был произведен в 1922 г. (несколько ранее аналогичный опыт был произведен П.Л. Капицей и Н.Н. Семеновым). Схема опыта показана на рис. 1.2. Из печки 1 выходит поток испарившихся молекул или атомов, на который действует магнитное поле электромагнита 2; диафрагмы 3 служат для создания узкого пучка; экран 4 представляет собой пластинку, на которой можно обнаружить следы осевших частиц. Поле электромагнита в одном из направлений должно быть неоднородным, что достигается специальной формой полюсных наконечников. В этом случае на атом, обладающий магнитным моментом m, направленным под углом q к направлению градиента поля по оси z, действует сила

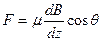, (1.14)

которая существует на участке длиной а. Движение на этом участке равномерно ускоренное. Поэтому отклонение (по оси z) в конце участка

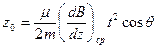, (1.15)

где m – масса атома, t – время пролета через поле на участке а.

В качестве испаряемого вещества Штерн и Герлах использовали серебро. В дальнейшем опыты были проделаны со щелочными металлами и атомарным водородом.

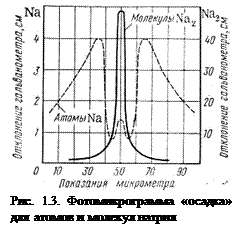На рис. 1.3 приведена фотомикрограмма «осадка» для атомов и молекул натрия.

При низких температурах большинство атомов образует молекулы Na₂, у которых результирующий магнитный момент равен нулю и отклонение отсутствует. Атомарное состояние характеризуется двугорбой кривой, т.е. на пластинке образуются две полоски, расположенные симметрично относительно среднего положения. Дублеты получаются не только для Na, но и для всех других атомов, имеющих один валентный электрон.

Это свидетельствует о пространственном квантовании магнитного момента. Действительно, если бы все значения были равновероятны, на пластинке образовалась бы сплошная полоса между точками 0’ и 0’’ (рис. 1.2); одна из этих точек соответствует значению q=0 (расположению магнитного момента параллельно полю), а вторая – значению q=180° (антипараллельному расположению магнитного момента и поля).

Опыт Штерна и Герлаха позволил рассчитать по формуле 1.13 проекцию магнитного момента атома на направление внешнего поля, которая оказалась равной магнетону Бора.

Модель Бора не объясняет результаты рассмотренного опыта. Известно, что атомы водорода, серебра, щелочных металлов и других элементов первой группы не обладают орбитальными механическими и магнитными моментами. Следовательно, для таких атомов вообще не должно наблюдаться отклонение в магнитном поле. Кроме того, по правилу пространственного квантования, если бы даже n_φ=1, магнитное квантовое число m в соответствии с возможными, по Бору, значениями cos α при n=1 должно равняться +1, 0, -1, т.е. на пластинке должны были образоваться три полоски вместо наблюдаемых двух. Модель Бора не объясняет также аномальный эффект Зеемана, тонкую структуру спектральных линий и многое другое.

Последовательное применение квантовой теории внесло поправки в некоторые из приведенных ранее формул квантования:

- квантование орбитального момента количества движения

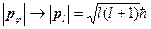(ср. 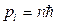) (1.16)

- квантование орбитального магнитного момента

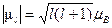(ср. 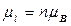) (1.17)

где l – орбитальное квантовое число, равное 0, 1, 2,... (n-1). Поскольку в квантовой механике нельзя говорить об определенной траектории, отпадает и необходимость исключения значения l=0. Здесь оно означает лишь сферически – симметричное распределение вероятности нахождения электрона в различных точках пространства;

- пространственное квантование магнитного и орбитального моментов

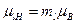(ср. 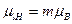), (1.18)

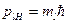
где m – орбитальное магнитное квантовое число, принимающее значения: -l, (-l+1), …, -1, 0, +1, …, (l-1), l; всего 2l+1 значений;

Одновременно с развитием квантовой теории и применением ее для объяснения явлений магнетизма было сделано значительное открытие, связанное с понятием спина.

В 1925 г. Гаудсимт и Юленбек высказали предположение о том, что электрон помимо заряда и массы обладает собственным моментом количества движения μ_s. Этой свойство электрона назвали спином, потому что согласно классической физике спиновые свойства электрона можно объяснить вращением его вокруг оси (от англ. to spin – вращаться). Спин свойственен всем микрочастицам.

В 1928 г. Создатель релятивистской квантовой теории П. Дирак показал, что свидетельство о наличии спина и его свойствах можно получить автоматически из теоретических выводов.

В соответствии с общими положениями квантовой механики собственный механический момент p _s выражается через спиновое квантовое число s:

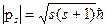(1.19)

При этом проекция момента на ось z может принимать 2s+1 значений в единицах ħ.

Рассмотрим результаты опытов Штерна – Герлаха и Эйнштейна – де Гааза с учетом введенных на основе квантовой механики поправок и понятия спина.

В опыте Штерна – Герлаха исследовались элементы первой группы, у которых атомы не обладают орбитальными магнитными моментами. Поэтому было непонятно отклонение пучка атомов в магнитном поле. Наличие спинового магнитного момента это объясняет. Нельзя было также понять, почему пучок атомов разбивается на два. Теперь стало ясно, что этому соответствуют возможные ориентации спина относительно оси z:

2s+1=2 (1.20)

Из формулы (1.18) следует, что s=1/2, т.е. спиновое квантовое число в отличие от орбитальных квантовых чисел является не целым, а полуцелым.

Наряду с механическим моментом электрон обладает собственным (спиновым) магнитным моментом μ_s. Опыт Штерна – Герлаха позволил непосредственно определить проекцию спинового магнитного момента на ось z, которая оказалась равной магнетону Бора. Это значит, что в соответствии с (1.16)

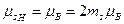, (1.21)

где m_s=±1/2. Введение спина объясняет результаты опытов Штерна и Герлаха. Действительно, хотя валентный электрон в атомах элементов первой группы находится в состоянии l=1, он обладает спиновым магнитным моментом. Проекция последнего может иметь два значения (μ_Н=±μ_В), что вызывает расщепление атомного пучка на два.

Магнитомеханические опыты показали, что

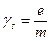, (1.22)

или в единицах e/2m

g_s=2 (1.23)

Но это возможно только в том случае, если

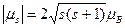(1.24)

Действительно, на основании формул (1.17), (1.22) и (1.5) имеем

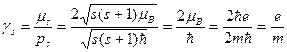. (1.25)

Ниже приведена сводная таблица орбитальных и спиновых моментов импульса и их проекций, а также магнитных моментов и их проекций.

Таблица. 1.1

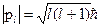
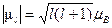
		l=1, 2, …, n-1
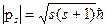
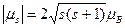
		s=1/2
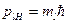
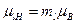
		ml= -l, …, 0, +l
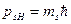
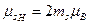
		ms=±1/2

Согласно квантово-механическим представлениям, при движении электрона в атоме существенны волновые свойства электрона. Каждому энергетическому состоянию соответствует волновая функция, квадрат модуля которой определяет плотность вероятности обнаружения электрона в окрестности данной точки пространства.

Вероятность обнаружения электрона в различных частях атома различна. Электрон при своем движении как бы «размазан» по всему объему, образуя электронное облако, плотность которого характеризует вероятность нахождения электрона в различных точках объема атома. Квантовые числа n иl характеризуют размер и форму электронного облака, а квантовое число m_l характеризует ориентацию электронного облака в пространстве.

На рис. 1.4 для примера приведено распределение электронной плотности (формы электронного облака) для s-, p-, d-состояний атома водорода, а на рис. 1.5 – наиболее вероятное местоположение электрона в 1s-, 2p- и 3d-состояниях, указываемое на рисунке увеличенной плотностью точек.

Электронные конфигурации и заполнение оболочек. Состояние движения изолированного электрона в кулоновском поле ядра атома характеризуется четырьмя квантовыми числами: n, l, m_l, m_s. Этими числами характеризуют состояние электрона и сложных атомов, в которых имеет место взаимодействие между электронами.

Совокупность электронов, обладающих одним и тем же квантовым числом n, образует оболочку атома. Оболочки атома при n=1, 2, 3, 4, 5, … обозначают соответственно буквами K, L, M, N, O и т. д.

Структура электронных оболочек сложных атомов объясняется на основе принципа запрета Паули, сформулированного в 1925 г.: в одном квантовом состоянии, определяющемся четверкой квантовых чисел n, l, m_l, m_s может находиться не более одного электрона.

Состояния с различными m_l и m_s в первом приближении энергетически равноценны. Состояния с различными l обладают разной энергией из-за различия в электрическом взаимодействии электронов. Схема нормальной последовательности квантовых состояний приведена в табл. 1.2.

Таблица 1.2

n	s	p	d	f	g
l=0 ml=0	l=1 ml=-1, 0, +1	l=2 ml=-2, -1, 0, +1, +2	l=3 ml= -3, -2, -1, 0, +1, +2, +3	l=4 ml= -4, -3, -2, -1, 0, +1, +2, +3, +4

Совокупность электронов с одним и тем же значением l называют слоем. Электронную конфигурацию атома записывают следующим образом: первым пишут число, обозначающее номер оболочки, второй – букву, обозначающую слой, в виде показателя степени у буквы указывают число электронов в данном слое. Например, 1s², 2s², 2p⁶ – это атом, который содержит два электрона в первом слое первой оболочки, два электрона в первом слое второй оболочки и шесть электронов во втором слое второй оболочки, что соответствует структуре неона.

Нормальный порядок заполнения не всегда имеет место, он нарушается, начиная с элемента калия. Это происходит вследствие того, что из-за взаимодействия электронов состояния с малыми n и большими l могут оказаться менее выгодными, чем состояния с большими n, но меньшим l. Вследствие этого у калия (Z=19) начинается постройка не 3d-, а 4s – состояния. Лишь после кальция (Z=20) со скандия (Z=21) начинается достройка 3d – электронного состояния, продолжающегося до никеля (Z=28). «Запоздалая» застройка имеет место не только для 3d – состояния, но также ряда других d- и f – слоев (4d, 4f, 5d, 6d). Элементы, в которых имеет место «запоздалая» достройка этих слоев, называют переходными. Всего в таблице Менделеева (исключая трансурановые элементы) имеется 42 переходных элемента. К ним относятся и три элемента Fe, Ni, Co.

Момент количества движения электронной оболочки атома. Анализ экспериментальных данных по характеру взаимодействия между электронами в атоме показывает, что большинстве случаев сила взаимодействия между спиновыми и орбитальными моментами всех электронов больше, чем сила взаимодействия между спиновым и орбитальным моментами каждого электрона. Такую связь называют связью Рассела – Саундерса. В этом случае полный момент количества движения электронной оболочки Р_J определяют следующим образом. Складывая орбитальные моменты всех электронов атома, находят суммарный орбитальный момент Р _L; складывая спиновые моменты, находят суммарный спиновый момент Р _S.

Полный момент количества движения электронной оболочки

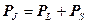(1.26)

Значения векторов Р _L, Р _S и Р _J можно представить в следующем виде:

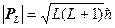; (1.28)

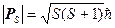; (1.26)

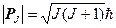, (1.29)

где L, S, J – квантовые числа, характеризующие соответствующие моменты.

Квантовое число L может иметь все целочисленные значения от суммы квантовых орбитальных чисел l_i для отдельных электронов, входящих в расчет, до их наименьшей алгебраической суммы. Например, в случае двух электронов с квантовыми числами l₁ и l₂ возможны (при l₁>l₂) следующие значения для L: l₁+l₂, l₁+l₂-1, …, l₁-l₂, всего 2l₂+1 значений.

Квантовой число S для атома, содержащего N электронов, может принимать следующие значения:

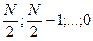при четном N,

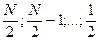при нечетном N.

Квантовое число J (суммарное внутренне квантовое число атома) принимает следующие значения: если L>S, то

J=L+S; L+S-1; …; L-S (всего 2S+1 значений);

если L<S, то

J=S+L; S+L-1; …; S-L (всего 2L+1 значений).

Магнитный момент электронной оболочки атома. Для определения полного магнитного момента необходимо найти его составляющие: суммарный спиновый магнитный момент

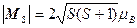, (1.30)

суммарный орбитальный магнитный момент

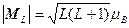(1.31)

и произвести их векторное суммирование:

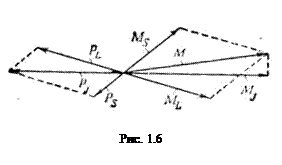M = M _L+ M _S. (1.32)

Найденный таким образом магнитный момент М в силу гиромагнитной аномалии спина (g_S=2g_L) не будет антипараллелен полному механическому моменту Р_J. Это иллюстрирует рис. 1.6, на котором масштабы выбраны так, что К₁ç М _Lç=К₂ç Р _Lç, тогда К₁ç М _Sç=2К₂ç Р _Sç и ç М ç не лежит на одной прямой с ç Р _Jç.

Составляющие М _L и М _S магнитного момента прецессируют вокруг направления Р _J (Р _J =const по значению и направлению). При этом перпендикулярные к Р _J составляющие моментов в среднем по времени за период вращения равны нулю, ибо они непрерывно меняют свое направление, и полный магнитный момент М _J электронной оболочки атома определяется только параллельными к Р _J составляющими моментов, т. е.

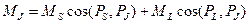; (1.33)

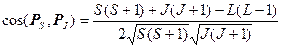; (1.33)

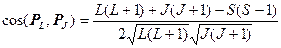. (1.34)

Отсюда

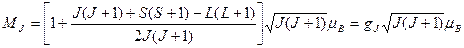, (1.36)

где

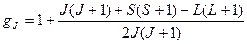(1.37)

называют фактором Ланде или g-фактором.

Для чисто орбитального момента S=0, J=L, g_J=g_L=1; для чисто спинового L=0, S=J, g_J=g_S=2; в общем случае g_J – дробное число, а при определенных соотношениях между L и S может быть равным нулю.

Векторы P _J и M _J подчиняются правилу пространственного квантования. При этом следует отметить, что проекция

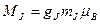, (1.38)

где m_J=J; (J-1);...; (-J+1); (-J) не является целым числом, кратным m_В, поскольку g_J в общем случае дробное число.

Определение полного магнитного момента атома существенно облегчается в связи с тем, что у заполненных слоев как орбитальные, так и спиновые магнитные моменты скомпенсированы. Поэтому при рассмотрении надо учитывать только не полностью заполненные слои.

§3. Элементы физики атомного ядра.

Дата добавления: 2014-01-07