Бипризма Френеля. Зеркало Ллойда

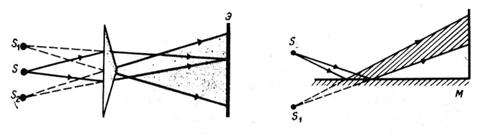
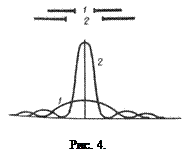
Рис. 3. Рис. 4.

§1.3. Расчет интерференционной картины от двух источников.

Этот расчет для рассмотренных выше методов наблюдения интерференции света можно провести, используя две узкие параллельные щели S₁ и S₂, расположенные очень близко друг к другу на расстоянии d (рис. 5). Они являются когерентными источниками – реальными или мнимыми изображениями источника в какой-то оптической системе. Рассмотрим результат интерференции в некоторой точке А экрана, параллельного обеим щелям и расположенного от них на расстоянии l (l>d). Начало отсчета выбрано в точке О, симметричной относительно щелей.

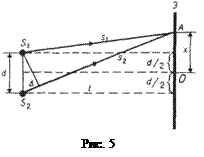Интенсивность в любой точке экрана, лежащей на расстоянии х от О, определяется оптической разностью хода Δ=s₂ - s₁. Из рис. 5. следует, что

,

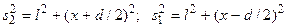откуда

,

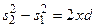или

.

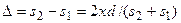Из условия l>>d следует, что s₁+s₂≈2l, поэтому

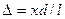. (4)

Подставив (4) в (2) и (3) получим, что максимумы интенсивности будут наблюдаться при

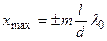(m=0, 1, 2, …) (5)

а минимумы – при

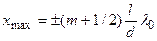(m=0, 1, 2, …) (6)

Расстояние между двумя соседними максимумами (или минимумами), называемое шириной интерференционной полосы, равно

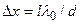, (7)

где Δх не зависит от порядка интерференции (величины m) и является постоянной для данных l, d и λ₀. Согласно формуле (7), Δх обратно пропорционально d; следовательно, при большом расстоянии между источниками, например при d≈l, отдельные полосы становятся неразличимыми. Для видимого света λ₀≈10^{-7 м, поэтому четкая интерференционная картина, доступная для наблюдения, имеет место при} l>>d (это условие и принимается в расчете).

Из выражений (5) и (6) следует, что интерференционная картина, создаваемая на экране двумя когерентными источниками света, представляет собой чередование светлых и темных полос, параллельных друг другу. Главный максимум, соответствующий m=0, проходит через точку О. Вверх и вниз от него на равных расстояниях друг от друга располагаются максимумы (минимумы) первого (m=1), второго (m=2) порядков и т. д.

Описанная картина, однако, справедлива лишь при освещении монохроматическим светом. Если использовать белый свет, то интерференционные максимумы для каждой длины волны, согласно формуле (7), смещены друг относительно друга и имеют вид радужных полос. Только для m=0 максимумы всех длин волн совпадают и в середине экрана будет наблюдаться белая полоса, по обе стороны которой симметрично расположатся спектрально окрашенные полосы максимумов первого, второго и т.д. порядков (ближе к полосе находятся зоны фиолетового цвета, дальше – зоны красного цвета).

Глава 2. Дифракция света.

§2.1. Зоны Френеля.

Дифракция света – это совокупность явлений, наблюдаемых при распространении света сквозь малые отверстия, вблизи границ непрозрачных тел и т.д. и обусловленных волновой природой света. Под дифракцией света обычно понимают отклонения от законов распространения света, описываемых геометрической оптикой.

Объяснение дифракции возможно с помощью принципа Гюйгенса, согласно которому каждая точка, до которой доходит волна, служит источников вторичных волн, а огибающая этих волн дает положение волнового фронта в следующий момент времени. Волновой фронт – это геометрическое место точек, до которых доходят колебания к некоторому моменту времени. Геометрическое место точек, для которых колебания имеют одинаковые фазы, называют волновой поверхностью. Волновой фронт также является волновой поверхностью.

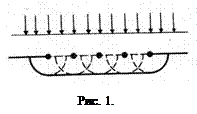Пусть для примера параллельный фронт волны (рассматриваем плоские волны) падает на отверстие в непрозрачном экране (рис. 1). Согласно Гюйгенсу, каждая точка выделяемого отверстием участка волнового фронта служит источником вторичных волн (в однородной изотропной среде они сферические). Построив огибающую вторичных волн для некоторого момента времени, видим, что фронт волны заходит в область геометрической тени, т.е. волны огибают края отверстия, иными словами, наблюдается явление дифракции.

Принцип Гюйгенса позволяет решать позволяет решать задачу лишь о направлении распространения волнового фронта, т.е. является принципом геометрическим. С его помощью можно, например, вывести законы отражения и преломления света на границе раздела двух сред. Однако принцип Гюйгенса не затрагивал по существу вопрос об амплитуде, а, следовательно, и об интенсивности распространяющихся за преградой световых волн. Кроме того, оставалось неясным, почему при распространении волны не возникает обратная волна.

Френель дополнил принцип Гюйгенса идеей интерференции вторичных волн. Согласно принципу Гюйгенса – Френеля, световая волна, возбуждаемая источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, «излучаемых» фиктивными источниками. Такими источниками могут служить бесконечно малые элементы любой замкнутой поверхности, охватывающей источник S. Обычно в качестве такой поверхности выбирают одну из волновых поверхностей, а поэтому все фиктивные источники действуют синфазно. Таким образом, для определения в некоторой точке пространства результирующей интенсивности надо учесть интерференцию всех этих вторичных волн.

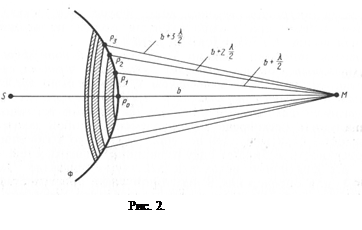
Пусть S – точечный источник монохроматического света (рис. 2), распространяющегося в однородной среде, а М – произвольная точка наблюдения, в которой определяется результирующая амплитуда световой волны, приходящей в эту точку. Согласно принципу Гюйгенса – Френеля, действие источника S заменяют действием воображаемых источников, расположенных на вспомогательной поверхности, в качестве которой выбрана волновая поверхность Ф.

Для определения результирующей амплитуды Френель предложил разбить волновую поверхность на кольцевые зоны, названные впоследствии зонами Френеля. Размеры кольцевых зон таковы, что разность хода лучей, идущих от соответственных точек каждой соседней зоны до точки наблюдения М, равна λ/2, т.е Р₁М-Р₀М=Р₂М-Р₁М=Р₃М-Р₂М=…=λ/2. Для этого необходимо из точки М построить сферы радиусами b+λ/2, b+2λ/2, b+3λ/2, …

Колебания, возбуждаемые в точке М двумя соседними зонами, противоположны по фазе, так как разность хода соответствующих лучей от этих зон до точки наблюдения М равна λ/2, а поэтому при наложении эти колебания будут ослаблять друг друга. Следовательно, амплитуда результирующего колебания, возбужденного в точке М всей совокупностью зон,

А=А₁-А₂+А₃-А₄+…, (1)

где А₁, А₂, … - амплитуды колебаний, возбуждаемых 1-й, 2-й, … зонами.

Действие отдельных зон на точку М тем меньше, чем больше угол φ_m между нормалью n к поверхности хоны и направлением на М. Таким образом, действие зон постепенно убывает от центральной зоны к периферическим. Кроме того, с ростом m уменьшается интенсивность излучения в направлении точки М (увеличивается расстояние от зоны до точки наблюдения). Следовательно, А₁>А₂>А₃>….

Так как общее число зон Френеля, умещающихся на полусфере огромно, а их площади очень малы, то в качестве допустимого возможно приближение: А_m=(A_m-1+A_m+1)/2. С учетом этого приближения из выражения (1) следует, что амплитуда результирующих колебаний в точке М А≈А₁/2. Таким образом, амплитуда результирующих колебаний в произвольной точке определяется как бы действием только половины центральной зоны Френеля. Поэтому, если на пути монохроматического света от точечного источника S поместить экран, закрывающий все зоны, кроме первой, то амплитуда в точке М увеличится по сравнению с полностью открытым волновым фронтом в два раза, а интенсивность – в четыре.

Дифракцию разделяют на два типа – в зависимости от расстояний от источника и точки наблюдения (экрана) до препятствия, расположенного на пути распространения света. Первый тип дифракции относится к случаю, когда на препятствие падает сферическая или плоская волна, а дифракционная картина наблюдается на экране, находящемся за препятствием на конечном от него расстоянии. Дифракционные явления этого типа впервые изучены Френелем и называются дифракцией Френеля (или дифракцией в сходящихся лучах). Этот тип дифракции будет подробно рассмотрен нами на практическом занятии.

Второй тип дифракции относится к случаю, когда на препятствие падает плоская волна, а дифракционная картина наблюдается на экране, находящемся в фокальной плоскости собирающей линзы, установленной за препятствием. Дифракционные явления этого типа изучены Фраунгофером и называются дифракцией Фраунгофера (или дифракцией в параллельных лучах).

§2.2.Дифракция Фраунгофера.

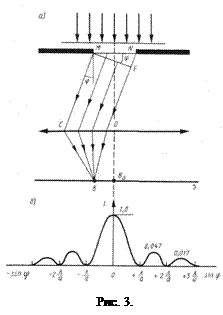Пусть плоская монохроматическая световая волна падает нормально на непрозрачный экран (рис. 3) с узкой щелью шириной а и длиной l>>a (т.е. щель бесконечно длинная). Дифракционная картина наблюдается на экране Э, находящемся в фокальной плоскости собирающей линзы, установленной на пути прошедшего через щель света. Плоскость щели и экран параллельны друг другу.

Согласно принципу Гюйгенса – Френеля, каждая точка щели является источником вторичных волн, колеблющихся в одинаковой фазе, поскольку плоскость щели совпадает с фронтом падающей плоской волны.

Параллельные пучки лучей, выходящие из щели в произвольном направлении φ (φ – угол дифракции), собираются линзой в точке В. Открытую часть волновой поверхности MN в плоскости щели разбивают на зоны Френеля, имеющие вид полос, параллельных ребру М и проведенных так, чтобы разность хода от их соответственных точек была равна λ/2. При этом на ширине щели умещается asinφ/(l/2) зон.

Если число зон Френеля четное, т.е

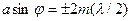(m=1, 2, 3,...),

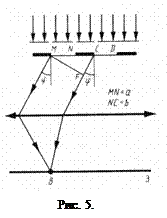
то в точке В наблюдается дифракционный минимум, если же число зон Френеля нечетное, т.е

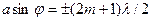(m=1, 2, 3,...),

то наблюдается дифракционный максимум, соответствующий действию одной некомпенсированной зоны Френеля. В направлении φ=0 наблюдается центральный дифракционный максимум, поскольку колебания, вызываемые в точке В₀ всеми участками щели, происходят в одной фазе.

На рис. (4) приведен дифракционный спектр – зависимость распределения интенсивности на экране от угла дифракции. Основная часть световой энергии сосредоточена в центральном максимуме. С увеличением угла дифракции интенсивность побочных максимумов резко уменьшается.

При освещении немонохроматическим светом боковые полоски радужно окрашены. С уменьшением ширины щели центральный максимум расширяется, при этом его яркость уменьшается. С увеличением ширины щели (а>l) дифракционные полосы становятся уже и ярче, а число полос больше. При а>>l в центре получается резкое изображение источника света.

В случае дифракции Фраунгофера на одной щели распределение интенсивности на экране определяется направлением дифрагированных лучей. Поэтому перемещение щели параллельно себе не изменит дифракционной картины. Следовательно, дифракционные картины, создаваемые каждой из двух щелей в отдельности, будут одинаковыми. результирующая картина определится как результат взаимной интерференции волн, идущих от обеих щелей.

Пусть плоская монохроматическая волна падает нормально на непрозрачный экран (рис. 5) с двумя одинаковыми щелями шириной а, отстоящими друг от друга на расстоянии b (a+b=d). очевидно, что минимумы будут на тех же местах, как и в случае одной щели, так как те направления, в которых ни одна из щелей не посылает света, не получат его и при двух щелях. Следовательно, прежние (главные) минимумы интенсивности наблюдаются в направлениях, определяемых условием

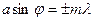(m=1, 2, 3,...).

Вследствие взаимной интерференции световых лучей, посылаемых двумя щелями, в некоторых направлениях они могут гасить друг друга, т.е. могут возникнуть дополнительные минимумы. Это будут, очевидно, направления, которым соответствует разность хода лучей l/2, 3l/2,..., посылаемых от соответственных точек обеих щелей (например, точек М и С). Такие направления (рис. 5) определяются условием

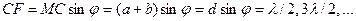. (2)

Таким образом, с учетом (2) условие дополнительных минимумов

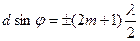(m=1, 2, 3,...).

В направлениях

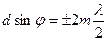(m=1, 2, 3,...)

действие одной щели усиливает действие другой, поэтому эти направления задают главные максимумы.

Таким образом, для двух щелей дифракционная картина определяется условиями

главные минимумы a sinφ= l, 2l, 3l,...

дополнительные минимумы d sinφ= l/2, 3l/2, 5l/2,...

главные максимумы d sinφ=0, l, 2l, 3l,...

т.е. между двумя главными максимумами располагается дополнительный минимум, а максимумы становятся более узкими, чем в случае одной щели.

Аналогично можно показать, что между каждыми двумя главными максимумами при трех щелях располагаются два дополнительных минимума, при четырех щелях – три и т.п. В случае N щелей число дополнительных минимумов, наблюдаемых между соседними главными максимумами, составит N-1.

Глава 3. Поляризация света. Распространение света в веществе.

§3.1. Основные сведения о поляризации.

Уравнения Максвелла полностью описывают возникновение, распространение и свойств электромагнитных волн. В частности, из них следует, что световые волны являются поперечными: векторы напряженностей электрического и магнитного полей световой волны взаимно перпендикулярны и колеблются перпендикулярно вектору скорости распространения волны (перпендикулярно лучу). Совокупность явлений волновой оптики, в которых проявляется поперечность световых электромагнитных волн, называют поляризацией света. Для описания поляризации исследуют поведение лишь одного векторов – вектора напряженности Е электрического поля, называемого световым вектором.

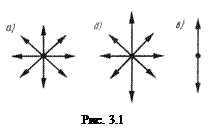
Атомы излучают световые волны независимо друг от друга, поэтому световая волна, излучаемая телом, характеризуется всевозможными равновероятными направлениями колебаний электрического вектора (рис. 3.1, а). Равномерное распределение векторов Е объясняется большим числом атомарных излучателей, а равенство амплитудных значений векторов Е – одинаковой (в среднем) интенсивностью излучения каждого из атомов. Свет со всевозможными равновероятными направлениями колебаний вектора Е (и следовательно Н) называют естественным (неполяризованным). Свет, в котором направления колебаний электрического вектора каким-то образом упорядочены, называют поляризованным. Так, если в результате каких-либо внешних воздействий появляется преимущественное (но не исключительное!) направление вектора Е (рис. 3.1, б), то имеем дело с частично поляризованным светом. Наиболее общим типом поляризованного света является эллиптически поляризованный – конец светового вектора описывает эллипс, лежащий в плоскости, перпендикулярной лучу. Свет, в котором вектор Е колеблется только в одном направлении, перпендикулярном лучу (рис. 3.1, в) называют плоскопляризованным (линейно поляризованным). Плоскость, проходящая через электрический вектор Е и луч, называется плоскостью поляризации.

Плоскополяризованный свет получают, пропуская естественный свет через поляризаторы, в качестве которых используются среды, анизотропные в отношении колебаний вектора Е, например кристаллы (в частности, турмалин). Поляризаторы можно использовать для анализа поляризованного света, тогда их называют анализаторами. Поляризаторы (анализаторы) свободно пропускают колебания, параллельные главной плоскости поляризатора (анализатора) - плоскости поляризации света, пропускаемого поляризатором, - и полностью или частично задерживают колебания, перпендикулярные ей.

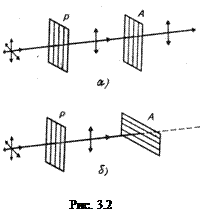
Пусть перпендикулярно на поляризатор Р (рис. 3.2, а) падает естественный свет. На рисунке поляризатор изображен в виде пластинки со штриховкой, параллельной главной плоскости поляризатора. Из поляризатора выходит плоскополяризованный свет. Чтобы в этом убедиться, на пути луча ставят анализатор А. Если главные плоскости Р и А параллельны друг другу, то поляризованный свет проходит через анализатор, если их главные плоскости перпендикулярны друг другу, то свет через анализатор не проходит (рис. 3.2, б).

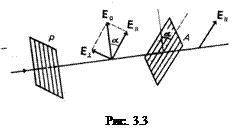
Если поляризатора и анализатор ориентированы произвольно, то интенсивность прошедшего через них света будет зависеть от угла a (рис. 3.3) между главными плоскостями анализатора и поляризатора. Обозначим амплитуду электрического вектора луча, прошедшего через поляризатор, через Е₀. Разложим вектор Е₀ на два компонента: параллельный главной плоскости анализатора и перпендикулярный ей. Это соответствует разложению волны, колеблющейся в плоскости Е₀ на две волны, поляризованные во взаимно перпендикулярных плоскостях и колеблющихся в одинаковой фазе. Одна из них (Е_||) пройдет через анализатор, а вторая (Е_^) будет погашена.

Если плоскополяризованный свет в амплитудой электрического вектора Е₀ падает на анализатор, то анализатор (рис. 3.3) пропустит только составляющую

Е_||=Е₀cosa. (3.1)

Так как интенсивность света пропорциональна квадрату амплитуды колебаний, то из (3.1) получаем

I=I₀cos²a, (3.2)

где I₀ – интенсивность плоскополяризованного света, падающего на анализатор, I - интенсивность света, вышедшего из анализатора. Уравнение (3.2) выражает закон Малюса, согласно которому интенсивность света, прошедшего последовательно через поляризатор и анализатор, пропорциональна квадрату косинуса угла между их главными плоскостями. Таким образом, интенсивность света, прошедшего через систему (3.3) изменяется от нуля (полное гашение света) при a=p/2 до I₀ при a=0.

Если пропустить естественный свет через два поляризатора, главные плоскости которых образуют угол a, то из первого выйдет плоскополяризованный свет, интенсивность которого I₀=1/2I_ест, из второго, согласно (3.2) выйдет свет интенсивностью I=I₀cos²a. Следовательно, интенсивность света, прошедшего через два поляризатора,

I=1/2I_естcos²a, (3.3)

откуда I_max=1/2I_ест (главные плоскости поляризаторов параллельны), I_min=0 (главные плоскости поляризаторов перпендикулярны).

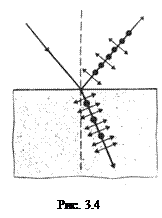
Явление поляризации света наблюдается при отражении и преломлении света на границе прозрачных изотропных диэлектриков. При падении естественного света на границу раздела двух изотропных диэлектриков (например, воздуха и стекла) часть его отражается, а часть преломляется и распространяется во второй среде. Оказалось, что отраженный и преломленный лучи частично поляризованы: при вращении анализатора вокруг лучей интенсивность света периодически усиливается и ослабевает (полного гашения не наблюдается). Эти опыты впервые были проведены Малюсом (1810). Дальнейшие исследования показали, что в отраженном луче преобладают колебания, перпендикулярные плоскости падения (на рис. 3.4 они обозначены точками), в преломленном – колебания, параллельные плоскости падения (на рисунке эти колебания изображены стрелками).

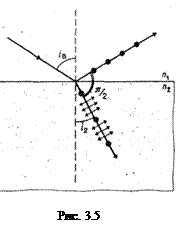Степень поляризации отраженного и проломленного света зависит от угла падения естественного света на границу раздела изотропных диэлектриков и показателя преломления. Брюстер (1815) установил закон, согласно которому при угле падения i_В (угол Брюстера), определяемым соотношением

tg i_B=n₂₁ (3.4)

(n₂₁ – показатель преломления второй среды относительно первой), отраженный луч является плоскополяризованным (содержит только колебания, перпендикулярные плоскости падения) (рис. 3.5). Преломленный же луч при угле падения i_В поляризуется максимально, но не полностью.

Двойное лучепреломление (впервые обнаружено в 1669 г. Бартолином для исландского шпата) – способность анизотропных веществ расщеплять падающий луч на два луча, распространяющихся в разных направлениях с различной фазовой скоростью и поляризованных во взаимно перпендикулярных направлениях. Анизотропия веществ – это зависимость их физических свойств от направления. Большинство кристаллов (кроме кристаллов кубической системы) анизотропны: их относительная диэлектрическая проницаемость и показатель преломления зависят от направления электрического вектора Е световой волны.

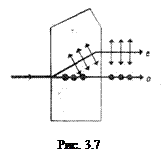
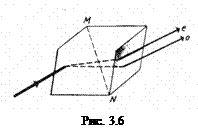В результате двойного лучепреломления при падении узкого светового пучка на достаточно толстый анизотропный кристалл из него выходят два пространственно разделенных луча, параллельных друг другу и падающему лучу (рис. 3.6). Даже в том случае, когда первичный пучок падает на кристалл нормально, преломленный пучок разделяется на два: один из них является продолжением первичного, а второй отклоняется (рис. 3.7). Первый из этих лучей со времен Гюйгенса называется обыкновенным (о), второй - необыкновенным (е).

В любом анизотропном кристалле имеется по крайней мере одно направление, в котором отсутствует двойное лучепреломление: падающий пучок света не раздваивается, и состояние поляризации не меняется. Это направление называется оптической осью кристалла. Любая прямая, проходящая параллельно данному направлению, является оптической осью кристалла, и пучок света, распространяясь вдоль нее, не испытывает двойного лучепреломления. В природе существуют одноосные и двуосные кристаллы. К первым относят исландский шпат, турмалин, кварц, ко вторым – слюда, гипс, топаз.

Исследования показывают, что обыкновенный и необыкновенный лучи плоскополяризованы во взаимно перпендикулярных плоскостях. Плоскость, проходящую через направление луча света и оптическую ось кристалла, называют главной плоскостью одноосного кристалла. Колебания электрического вектора в обыкновенном луче происходят перпендикулярно главной плоскости (следовательно, перпендикулярно оптической оси), в необыкновенном – в главной плоскости (следовательно, электрический вектор необыкновенного луча образует с оптической осью некоторые углы).

Двойное лучепреломление – следствие анизотропии диэлектрической проницаемости e в кристаллах: в направлении оптической оси и в направлениях, перпендикулярных ей, e имеет различные значения, а в других направлениях e имеет промежуточное значение.

Экспериментально обнаружено, что оптически изотропные вещества становятся анизотропными, если они подвергаются механическим напряжениям (Брюстер, 1816), помещаются в электрическое (Керр, 1875) или магнитное (Коттон и Мутон, 1905) поле. В результате вещество приобретает свойства одноосного кристалла, оптическая ось которого совпадает соответственно с направлениями деформации, электрического или магнитного поля.

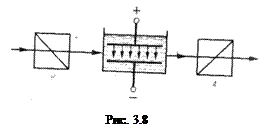На рис. 3.8 для примера приведена принципиальная схема, используемая для изучения эффекта Керра – оптической анизотропии прозрачных веществ под воздействием однородного электрического поля. Ячейка Керра, например, кювета с жидкостью, в которую введены пластины конденсатора, помещается между скрещенными поляризатором и анализатором. При отсутствии электрического поля свет через систему не проходит. При наложении электрического поля среда становится анизотропной и выходящий из ячейки свет оказывается эллиптически поляризованным и частично проходит через анализатор. Эффект Керра обусловлен различной поляризуемостью молекул диэлектрика по разным направлениям. Электрическое поле ориентирует полярные молекулы вдоль поля и индуцирует электрический момент у неполярных молекул. В результате этого показатели преломления становятся различными и возникает двойное лучепреломление. Эффект Керра безынерционен: переход вещества из изотропного состояния в анизотропное при включении (выключении) электрического поля составляет ~10^-10 с. Поэтому ячейка Керра - идеальный затвор, применяемый в быстропротекающих процессах (звукозапись, скоростная фото- и киносъемка и т.д.).

В случае анизотропных молекул среды, обладающих магнитными моментами, их преимущественная ориентация может быть создана постоянным магнитным полем. Поэтому в сильных магнитных полях среда становится анизотропной и в ней наблюдается двойное лучепреломление. В этом состоит эффект Коттона – Мутона.

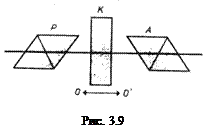Если между скрещенным поляризатором Р и анализатором А поместить пластинку К из кристаллического кварца (одноосный кристалл), вырезанную перпендикулярно оптической оси, и если свет распространяется вдоль оптической оси (рис. 3.9), то двойное лучепреломление отсутствует, а следовательно, свет через систему проходить не должен. Однако, как показал опыт (Араго, 1811), все-таки свет через систему проходит. При повороте анализатора на угол φ он вновь перестает пропускать свет. Следовательно, свет после прохождения кварца остается плоскополяризованным, но кварц поворачивает плоскость поляризации света на угол φ. Это явление называют вращением плоскости поляризации (или оптической активностью). Вещества (например, из твердых тел – кварц, сахар, киноварь, из жидкостей – водный раствор сахара, винная кислота, скипидар), обладающие способностью в отсутствие внешних воздействий вращать плоскость поляризации, называют оптически активными. Угол поворота плоскости поляризации для оптически активных кристаллов и чистых жидкостей

φ=ad

для оптически активных растворов

φ=[a]Сd

где d – расстояние, пройденное светом в оптически активном веществе, a [a] – удельное вращение, численно равное углу поворота плоскости поляризации света слоем оптически активного раствора единичной толщины (единичной концентрации – для растворов), С – массовая концентрация оптически активного вещества в растворе (кг/м³). Удельное вращение зависит от природы вещества, температуры и длины волны света в вакууме.

Фарадей (1845) обнаружил вращение плоскости поляризации в оптически неактивных веществах под действием магнитного поля. Это явление называют эффектом Фарадея (или магнитного вращения плоскости поляризации). Знак вращения в данном случае зависит только от направления распространения света, что отличает вращение плоскости поляризации в магнитном поле от оптической в отсутствие внешних воздействий. В эффекте Фарадея впервые обнаружена связь между оптическими и магнитными явлениями.

§3.2. Дисперсия света. Поглощение света. Рассеяние света.

Дисперсия света – зависимость фазовой скорости света в среде от его частоты. Так как v=c/n, то показатель преломления среды оказывается зависящим от частоты ν (длины волны λ). Эта зависимость обнаруживается при прохождении пучка белого света через призму из какого-либо прозрачного материала: на экране, установленном за призмой, наблюдается призматический спектр – полоса, окрашенная в непрерывно чередующиеся света радуги – от красного до фиолетового. Таким образом, призма может служить спектральным прибором.

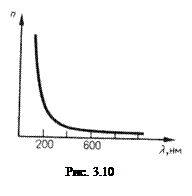
На рис. 3.10 приведена качественная зависимость n от λ для прозрачных веществ: n увеличивается с уменьшением λ. Такую зависимость n от λ называют нормальной дисперсией: 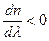. Если 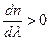, то дисперсию света называют аномальной. Она наблюдается вблизи полос поглощения вещества.

Количественной характеристикой дисперсии света является физическая величина D_λ=dn/dλ, называемая дисперсией показателя преломления.

Спектры, получаемые с помощью призмы и дифракционной решетки, резко различны: 1) дифракционная решетка разлагает свет непосредственно по длинам волн, а призма – по значениям показателя преломления; 2) составные цвета в обоих спектрах располагаются по разному: красные лучи имеют большую длину волны, чем фиолетовые, поэтому отклоняются дифракционной решеткой сильнее, а призмой - слабее, так как для них показатель преломления меньше.

Согласно классической электронной теории, дисперсия света рассматривается как результат взаимодействия электромагнитных волн с заряженными частицами вещества, совершающими вынужденные колебания в переменном электромагнитном поле волны. Формально дисперсия света – следствие зависимости 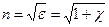(ε и χ – соответственно диэлектрические проницаемость и восприимчивость среды) от частоты световых волн. Так как χ=Р/(ε₀Е), где Р – мгновенное значение поляризованности, Е – модуль вектора напряженности электрического поля, создающего поляризованность Р в данной точке диэлектрика, то

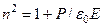. (3.5)

В данном случае основную роль играет электронная поляризация, т.е. вынужденные колебания электронов под действием электрической составляющей поля волны, так как для ориентационной поляризации молекул частота колебаний в световой волне очень высока.

Напряженность поля, действующего на электрон молекулы, вообще говоря, отличается от напряженности поля световой волны, так как в действительности в любой заданной точке вещества возникает дополнительное поле, создаваемое всеми окружающими, тоже поляризованными молекулами. Однако в случае газообразной среды это дополнительное поле пренебрежимо мало и под Е в соотношении (3.5) можно понимать напряженность электрического поля световой волны. Поэтому дальнейшее рассмотрение будем проводить при этом допущении, справедливом только для газообразных сред.

Электроны, входящие в атом, делятся на внешние, или оптические, и электроны внутренних оболочек. С излучением оптического диапазона взаимодействуют только внешние электроны, поскольку собственные частоты электронов внутренних оболочек настолько велики, что их колебания в поле световой волны практически не возбуждаются. Поэтому электронная теория дисперсии рассматривает только оптические электроны.

Для упрощения рассмотрим колебания только одного оптического электрона. Наведенный дипольный момент электрона, совершающего вынужденные колебания, равен р=ех. Если концентрация атомов среды равна n₀, то мгновенное значение поляризованности

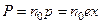_. (3.6)

Из (3.5) и (3.6) получим

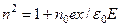. (3.7)

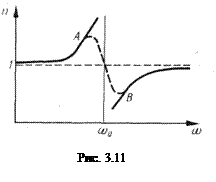Таким образом, задача сводится к определению смещения электрона под действием внешнего поля Е, которое в монохроматической волне изменяется со временем по гармоническому закону: Е=Е₀cosωt.

Дифференциальное уравнение вынужденных колебаний оптического электрона (предполагается, что среда света не поглощает, а следовательно, не учитывается сила сопротивления, обусловливающая поглощение энергии падающей волны)

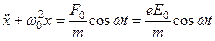. (3.8)

Решением уравнения (3.8) является

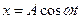(3.9)

где

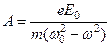(3.10)

В чем легко убедиться подстановкой. Подставляя (3.9) и (3.10) в (3.7), получаем

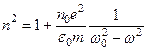(3.11)

Таким образом, показатель преломления зависит от частоты внешнего поля, т.е. выражение (3.11)действительно подтверждает явление дисперсии света. График зависимости n от ω представлен на рис. 3.11. Подобное поведение показателя преломления вблизи собственной частоты получилось в результате допущения об отсутствии сил сопротивления при колебаниях электронов. Если принять в расчет и это обстоятельство, то график функции n(ω) вблизи ω₀ задается пунктирной линией АВ. Область АВ – область аномальной дисперсии, остальные участки зависимости n(ω)описывают нормальную дисперсию.

Поглощение света – явление уменьшения энергии световой волны при ее распространении в веществе вследствие преобразования энергии волны в другие виды энергии.

Поглощение света подчиняется закону Бугера – Ламберта:

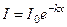
где I₀ и I – интенсивности плоской волны монохроматического света на входе и на выходе слоя поглощающего вещества толщиной х, k - натуральный показатель поглощения, зависящий от длины волны, химической природы и состояния поглощающего вещества. В основе закона Бугера – Ламберта лежит основной принцип линейной оптики – независимость характера оптических явлений от интенсивности света. Поэтому этот закон выполняется для слабых световых потоков.

Для разбавленного раствора поглощающего вещества в непоглощающем растворителе выполняется закон Бера: k=bc, где с – концентрация раствора, а b – коэффициент пропорциональности, не зависящий от с. В концентрированных растворах закон Бера нарушается из-за влияния взаимодействия между близко расположенными молекулами поглощающего вещества.

Зависимость натурального показателя поглощения диэлектрика от длины волны света, характеризующая спектр поглощения света в этой среде, связана с явлением резонанса при вынужденных колебаниях электронов в атомах и атомов в молекулах диэлектрика. Диэлектрики поглощают свет более или менее селективно: поглощение велико лишь в областях частот, близких к частотам собственных колебаний электронов в атомах и атомов в молекулах. Наиболее четко это явление резонансного поглощения света обнаруживается у разреженных одноатомных газов (например, паров металлов), для которых характерен линейчатый спектр поглощения света. Дискретные частоты интенсивного поглощения света совпадают с частотами собственного излучения возбужденных атомов этих газов.

У газов с многоатомными молекулами наблюдаются системы тесно расположенных линий, образующих полосы поглощения. Структура полос поглощения определяется составом и строением молекул. Жидкие и твердые диэлектрики имеют сплошные спектры поглощения, состоящие из сравнительно широких полос поглощения, в пределах которых натуральный показатель поглощения k достигает значительной величины и плавно изменяется в зависимости от длины волны. Такой ход зависимости k от λ у конденсированных сред объясняется сильным взаимодействием между частицами среды, приводящим к появлению множества дополнительных резонансных частот.

При достаточно больших значениях интенсивности света закон Бугера – Ламберта нарушается: показатель поглощения диэлектрической среды начинает зависеть от I, уменьшаясь с ростом I. Это явление, необъяснимое в рамках классической теории поглощения света, легко истолковывается в квантовой теории взаимодействия света с веществом. При поглощении света часть молекул среды переходит в возбужденное состояние. Возбужденные молекулы не могут участвовать в дальнейшем поглощении света до тех пор, пока они не вернутся, растратив свою избыточную энергию, в невозбужденное (нормальное) состояние. Доля возбужденных молекул среды тем больше, чем больше интенсивность света и чем больше среднее время жизни молекулы в возбужденном состоянии. Если доля этих молекул незначительна, то поглощение света происходит в соответствии с законом Бугера – Ламберта. В противном случае k уменьшается с ростом интенсивности света.

Можно осуществить такое неравновесное состояние среды, при котором доля возбужденных молекул будет столь велика, что натуральный показатель поглощения среды станет отрицательным. Это явление используется в квантовых генераторах радиоволн и света (лазеры и мазеры).

Рассеяние света – это процесс преобразования света веществом, сопровождающийся изменением направления распространения света и появлением несобственного свечения вещества.

Л.И. Мандельштам объяснил рассеяние света в средах нарушением их оптической однородности, при котором показатель преломления среды не постоянен, а изменяется от точки к точке. Такими средами являются мутные среды – среды, в которых взвешено множество очень мелких частиц инородных веществ: аэрозоли (облака, дым, туман), эмульсии, коллоидные растворы и т.д.

Если расстояние между малыми по размеру неоднородностями мутной среды значительно больше длины волны света, то свет, проходя через мутную среду, дифрагирует от беспорядочно расположенных микронеоднородностей – независимых «вторичны» источников, - давая равномерное распределение интенсивностей по всем направлениям, т.е. оптически неоднородная среда рассеивает свет по всем направлениям.

Если размеры частиц мутной среды малы по сравнению с длиной волны света, то такое рассеяние света получило название эффекта Тиндаля (1869). Этот эффект можно наблюдать, например, когда узкий пучок солнечных лучей, проходя через запыленный воздух, рассеивается на пылинках и становится видимым. Теория эффекта Тиндаля дана Рэлеем. Закон Рэлея (1871): интенсивность рассеянного света обратно пропорциональна четвертой степени длины волны возбуждающего света (I~l^-4).

М. Смолуховский (1908) указал, что причиной рассеяния света могут быть также флуктуации плотности, возникающие в процессе хаотического теплового движения молекул среды. Рассеяние света в чистых средах, обусловленное флуктуациями плотности, анизотропии или концентрации, называют молекулярным. Оно также подчиняется закону Рэлея.

Молекулярным рассеянием объясняется, например, голубой цвет неба. Согласно закону Рэлея, интенсивность рассеянного света обратно пропорциональна четвертой степени длины волны, поэтому голубые и синие лучи рассеиваются сильнее, чем желтые и красные, обусловливая цвет неба. По этой же причине свет, прошедший через значительную толще атмосферы, оказывается обогащенным более длинными волнами и поэтому при закате и восходе Солнце кажется красным. Флуктуации плотности и интенсивность рассеяния света возрастают с увеличением температуры. Поэтому в ясный летний день цвет неба является более насыщенным по сравнению с таким же зимним днем.

Дата добавления: 2014-01-07