Случайные события. Основные понятия. Действия над событиями

Почти в каждой области человеческой деятельности приходится иметь дело с наблюдениями, экспериментами, совершаемыми с многократным повторением, и при практически неизменных внешних условиях.

Испытание – комплекс условий, который может быть воспроизведен сколь угодно много раз.

Событие – результат, исход испытания. Требование к теоретико-вероятностному эксперименту: задание множества возможных исходов отдельного испытания, но при этом до получения результата нельзя предсказать, какой именно из исходов осуществится. Событие, которое в результате испытания может произойти или не произойти называется случайным (Обозначается буквами A,B,C,D…).

Достоверное событие обязательно происходит в результате данного испытания (обозначается буквой U).

Невозможное событие не может произойти в результате данного испытания (обозначается буквой V или Æ).

Сумма (объединение) событий A и B – такое событие, которое заключается в осуществлении хотя бы одного из них (или A или B или A и B вместе) (обозначается A+B или AÈB).

Произведение (пересечение) событий A и B – событие, которое заключается в их совместном осуществлении (обозначается AB или AÇB).

Несовместные события A и B – в результате данного испытания их совместное осуществление невозможно, т. е. AB=Æ.

Особый интерес представляет полная группа попарно несовместных событий – такая совокупность событий, что A₁+A₂+A3+¼+A_n=U и A_iA_j=Æ, при i¹j. Говорят, что U распадается на n частных случаев. Очевидно, что всякая такая группа может быть разбита на непересекающиеся подмножества.

Противоположными называют два несовместных события A и B, образующих полную группу, т. е. AB=Æ и A+B=U (обозначается B=`A).

§3 Классическое и статистическое определение вероятности случайного события.

а) Классическое определение вероятности случайного события (Лаплас).

Пусть достоверное событие U распадается на n равновозможных 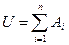, сумма m из которых, дает событие А. Тогда принято говорить, что в данном испытании имеется n случаев, из которых m благоприятствует появлению события А. Вероятностью события А называют отношение числа m случаев, благоприятствующих событию А, к числу n всех равновозможных событий:

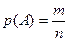
Свойства вероятности:

1). 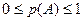, так как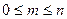

2). Вероятность достоверного события равна 1; p(U)=1, так как для U m=n.

3). Вероятность невозможного события равна 0; p(Æ)=0, так как для V m=0.

б) Статистическое определение вероятности.

Пусть серию из n испытаний проводят в одних и тех же условиях. Причем интересующее нас событие А осуществилось m раз. Тогда m называют частотой события А, а отношение:

называют относительной частотой события А (частостью)

Экспериментальным фактом является то, что 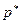при большом числе испытаний обнаруживает свойство стабильности, группируется около определенного значения, и при , 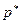представляет собой статистическую вероятность события А, или:

Дата добавления: 2014-01-07