Вычисление обратной матрицы

Определение параметров шероховатости

Наиболее простым и доступным средством оценки шероховатости поверхности являются наборы образцов шероховатости в виде пластин для разных методов обработки: точения, фрезерования, строгания, шлифования и т. д.

Образцы шероховатости служат для оценки шероховатости по параметру Ra методом сравнения.

Более достоверно можно измерить шероховатость с помощью микроскопов.

Двойной микроскоп академика Линника МИС-11 предназначен для измерения шероховатости поверхности методом светового сечения.

Сущность метода заключается в том, что световой поток, проходящий через узкую прямоугольную щель и направленный на исследуемую поверхность под некоторым углом, как бы сечет её плоскостью перпендикулярно к следам обработки. Изображение щели, отражаясь от поверхности претерпевает искривление, характеризующее конфигурацию поверхности. По форме и размеру изгиба изображения щели судят о неровностях поверхности. Микроскоп МИС-11 позволяет измерять высоты микронеровностей в пределах 6,3 ¸ 62,5 мкм и 3,2 ¸ 18,7 мкм, в зависимости от фокусного расстояния сменного объектива. Допускаемая погрешность составляет 7,5-18%.

Микроинтерферометр модели МИИ4 предназначен для измерения профильным методом неровностей поверхности высотой от 0,03 до 1 мкм.

Действие прибора основано на явлении интерференции света. Прибор позволяет измерять параметры шероховатости Rz, Rmax в пределах 0,05−0,8 мкм.

Суммарная погрешность среднего из трех измерений составляет 5 ¸ 15%.

Для определения параметров шероховатости поверхности используют профилограммы профиля поверхности исследуемого образца полученные с помощью профилографов (например, профилографа-профилометра мод. 201), которые ощупывают профиль поверхности специальной алмазной иглой. Для оценки параметров шероховатости на профилограмме проводят среднюю линию, а также линии выступов и впадин. Все параметры определяются относительно средней линии.

Современные приборы профилометры автоматически определяют все численные параметры шероховатости поверхности и результаты записывают на ленту и демонстрируют на экране.

Например, профилометр мод. 253 измеряет параметр шероховатости R_a в пределах 2,5−0,04 мкм с основной приведенной погрешностью до 16%, профилометр под. 283 измеряет R_a в пределах 10−0,02 мкм, профилограф-профилометр мод. 252 (с цифровым отсчетом) измеряет R_a в пределах 100−0,02 мкм, R_max в пределах 200−0,1 мкм, S_m в пределах 12,5−0,003 мм, t_p в пределах 100−0%.

Пусть A = (a_ij) – квадратная матрица с определителем, не равным нулю. Тогда существует обратная матрица A ^–1, которая вычисляется по формуле

.

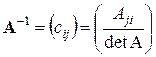Последняя формула означает, что в i -й строке и j -м столбце обратной матрицы располагается алгебраическое дополнение элемента, стоящего в j -й строке и в i -м столбце исходной матрицы, деленное на определитель исходной матрицы.

Напомним здесь, что A_pq = (–1) ^{p + q} M_pq, где M_pq называется минором и представляет собой определитель, получающийся из определителя det A вычеркиванием p -й строки и q -го столбца.

Если определитель матрицы равен нулю, матрица называется вырожденной.

Пример 1. Построить матрицу, обратную к заданной матрице

.

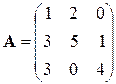Вычислим детерминант матрицы: detA = 20 + 6 – 24 = 2.

Построим матрицу , каждый элемент которой есть алгебраическое дополнение соответствующего элемента матрицы А:

.

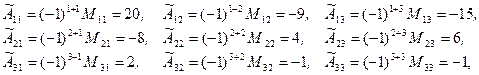
Транспонируем полученную матрицу: .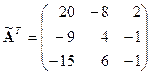

Выпишем обратную матрицу: .

Пример 2. Проверьте равенства AA ^–1 = A ^–1 A = E в предыдущем примере.

.

Дата добавления: 2014-01-07