Понятия экстремума и оптимума функции одной переменной

Для случая функции одной переменной и a Ј x Ј b на рис.1 показаны все три вида точек: A, B, C - стационарные точки, D, E, F - точки разрыва производной, a, b - граничные точки. При этом в точке D имеем глобальный максимум, а в точке a - глобальный минимум.

Рис. 1

Очевидно, что не всякая "подозрительная" точка представляет интерес. Среди точек первых двух видов следует отбраковать те, в которых нет экстремума (например, точки B и E на рис.1) и которые не соответствуют искомому типу экстремума. С этой целью используются достаточные условия экстремума.

Для функции одной переменной имеется несколько вариантов достаточных условий. Если f (x^* ± e) > f (x^*), где e - малая положительная величина, в точке x^* имеем локальный минимум. Сменив знак неравенства на обратный, получим условие максимума. Второй вариант заключается в проверке знака первой производной в точках (x ^*- e) и (x^*+e): смена знака с минуса на плюс указывает на минимум, а с плюса на минус - на максимум. Наконец, для дважды дифференцируемой функции в точке x^* - минимум, если вторая производная положительна, и максимум, если она отрицательна. Для непрерывно дифференцируемой функции точке x^* соответствует экстремум, если в ней порядок первой ненулевой производной четный (в частности, второй).

При исследовании функции одной переменной могут оказаться полезными следующие простые свойства. У непрерывной функции максимумы и минимумы чередуются между собой. Поэтому, если между установленными точками максимума и минимума (или наоборот) имеется одна "подозрительная" точка, то в ней экстремума нет. Если функция строго возрастает на интервале , т.е. df / dx >0 на всем интервале, то x^*_max = b, а x^*_min = a. Это справедливо и при нестрогом возрастании, но тогда решение может быть не единственным. Если производная положительна в точке a, то x^*_max № a, если же она отрицательна, то x^*_min № a.

Определение экстремума облегчается, когда функция обладает свойством выпуклости или вогнутости. Это свойство устанавливается с помощью различных соотношений. Для одномерного случая справедливы следующие определения.

Функция f (x) выпукла на интервале [ a, b ], если для любых точек x ₁, x ₂О[ a,b ] выполняется неравенство

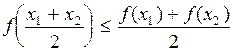. (1)

Функция f (x) выпукла на интервале [ a, b ], если для любых точек x ₁, x ₂О[ a,b ]и произвольного числа qÎ [0, 1] выполняется неравенство

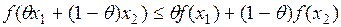. (2)

Дважды дифференцируемая на интервале [ a, b ] функция f (x) выпукла, если на этом интервале

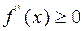. (3)

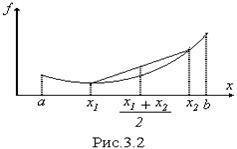Условия (1),(2) не требуют дифференцируемости функции. Их геометрический смысл иллюстрируется рис.2. Для выпуклой функции хорда, соединяющая две произвольные точки графика функции, лежит не ниже этой части графика. По условию (1) это устанавливается проверкой только в точке (x ₁ +x ₂ ) /2, а согласно (2) при изменении q от 0 до 1 мы движемся от точки x ₂ к точке x ₁ одновременно по графику функции (левая часть неравенства) и по хорде (правая часть неравенства), то есть проверка осуществляется на всем отрезке [ x _1, x ₂].

Изменение знаков неравенств в (1)-(3) на противоположные приводит к определению вогнутой функции. Если знаки неравенств заменить строгими, исключить случай x ₁ = x ₂ и граничные значения q, то получим определение строго выпуклой или строго вогнутой функции. Очевидно, что если f (x) выпукла, то - f (x) – вогнута, и наоборот.

В теории оптимизации наиболее употребительно второе определение выпуклости. Оно легко обобщается на n -мерные функции: функция f (X) выпукла на выпуклом множестве D, если для любых двух точек X⁽¹⁾,X⁽²⁾О D и произвольного числа q Î[0,I] выполняется неравенство

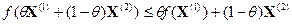, (4)

где X⁽¹⁾,X⁽²⁾ - n -мерные векторы переменных.

Рассмотрим пример. Покажем, что функция f (x)= x ² выпукла на интервале [-1,1]. Для этой функции условие выпуклости (2) принимает вид

.

Справедливость данного неравенства для q =0 и q =1 очевидна. Теперь докажем, что оно выполняется и для 0< q <1. Возведя в квадрат левую часть и сделав элементарные преобразования, получим

или

.

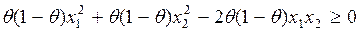Так как q (1- q)№0, то из этого неравенства следует

или ,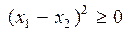

что всегда справедливо, а при x ₁№ x ₂ имеем строгое неравенство. Таким образом, функция f (x)= x ² является строго выпуклой.

Приведем некоторые полезные свойства выпуклых (вогнутых) функций на выпуклом множестве D.

1. Если функции f ₁, f ₂,..., f _m выпуклы на выпуклом множестве D и числа C ₁, C ₂,..., C _m не отрицательны, то функция также выпукла на D.

2. Если функции f ₁, f ₂,..., f _m выпуклы на множестве D, то выпукла на D и функция f (X)= f_i (X).

3. Если функция f (X) выпукла на множестве D, то для любого числа 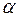множество {XО D | f (X)Јa} является выпуклым.

4. Функция f (X), строго выпуклая (вогнутая) на D, имеет не более одного локального минимума (максимума). Любой локальный минимум (максимум) является глобальным.

5. Функция f (X), строго выпуклая (вогнутая) на D, достигает наибольшего (наименьшего) значения на границе множества D.

Дата добавления: 2014-01-07