Понятия экстремума и оптимума функции нескольких переменных

Теперь остановимся на особенностях исследования функций многих переменных. Определение стационарных точек даже функции одной переменной может вызвать затруднения, если необходимое условие приводит к сложному нелинейному уравнению (например, транс-цендентному). При n переменных необходимые условия дают систему n уравнений, в общем случае нелинейных. Решение системы нелинейных уравнений представляет собой самостоятельную сложную задачу, и здесь не обойтись без методов нелинейного программирования. Но последние можно применить непосредственно к функции, не используя необходимые условия, что нередко оказывается более эффективным.

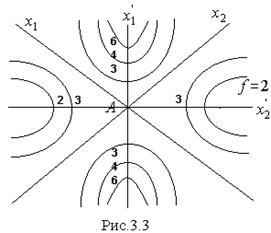
Если стационарные точки найдены, то из них нужно выделить те, в которых функция имеет экстремум искомого типа. При этом недостаточно исследовать поведение функции по отдельным переменным. Так, например, для функции двух переменных малые отклонения от стационарной точки A как по x ₁,так и x ₂ приводят к уменьшению значения функции (рис.3.3), что, казалось бы, указывает на наличие в этой точке максимума. Однако в точке A нет ни максимума, ни минимума. Действительно, если повернуть оси координат на , то при отклонении по x ₁ў функция возрастает, а по x ₂ў - убывает. Такую точку называют седловой (аналог точки перегиба функции одной переменной). Точно так же в случае функции многих переменных стационарная точка является седловой, если функция ведет себя по-разному в окрестности этой точки. Таким образом, для установления экстремума необходимо исследовать всю окрестность стационарной точки, что можно сделать с помощью ряда Тейлора. В нем слагаемые первого порядка содержат первые производные, которые в стационарной точке равны нулю; слагаемые порядка выше второго стремятся к нулю быстрее слагаемых второго порядка. Следовательно, локальные свойства функции определяются производными второго порядка. Опуская выкладки, приведем достаточные условия экстремума в окончательном виде.

Составим квадратную матрицу n -го порядка из вторых частных производных (матрицу Гессе или гессиан):

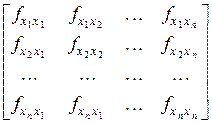
где 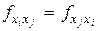- частные производные функции f (X) по x_i и x_j в исследуемой стационарной точке. В стационарной точке имеем локальный минимум, если все диагональные определители матрицы Гессе положительны, то есть

D _i >0, i =1, n (5)

и локальный максимум, если

D _i <0, i =1,3,5,..., D _i >0, i =2,4,6,... (6)

В частности, для функции двух переменных условия минимума (5) имеют вид

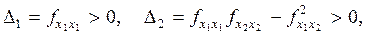(7)

а условия максимума (6)

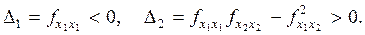(8)

Из приведенных выражений видно, что увеличение размерности функции ведет к непропорционально увеличивающемуся объему вычислений, необходимых для проверки достаточных условий. Еще большие трудности возникают при исследовании точек разрыва производных. Поэтому на практике часто отказываются от проверки достаточных условий, а точку глобального экстремума находят прямым сравнением значений функции во всех критических точках.

При решении задач на условный экстремум приходится выявлять также "подозрительные" точки третьего вида - точки на границе допустимой области. В задачах с одной переменной граница D - это точки на концах интервала, а в многомерном случае граница представляет собой линию или поверхность и ее исследование с целью выявления экстремальных точек становится весьма проблематичным.

Проиллюстрируем это на примере следующей задачи:

f (X) ® min, (9)

j ₁(X)і0, (10)

j ₂(X)і0, (11)

j ₃(X)і0. (12)

Как решать такую задачу? Сначала найдем все точки, в которых может быть экстремум. Для этого нам потребуется решить ряд задач меньшей размерности.

Задача 1: найти экстремальные точки (далее - э.т.) внутри допустимой области. С этой целью решаем задачу на безусловный экстремум: f (X) ® min. Предположим, что необходимые условия экстремума дают систему уравнений, которая поддается решению, и мы находим все э.т. Из них оставим только те, которые удовлетворяют условиям (10)-(12). Можно также отсеять точки, в которых не минимум, но для этого надо проверять достаточные условия.

Задача 2: найти э.т. на границе допустимой области, порождаемой ограничением (310). Для этого нужно решить задачу на условный экстремум

f (X)® min, j ₁ (X)=0.

Здесь возможны два подхода: метод исключения и метод множителей Лагранжа. Применим первый из них (второй будет рассмотрен в следующем разделе). Из условия-равенства выразим одну переменную через остальные и подставим в f (X). Таким образом, задачу на условный экстремум с n переменными сводим к задаче на безусловный экстремум с n -1 переменной. Снова предположим, что нам удается разрешить систему необходимых условий для этой задачи и найти ее э.т. Оставляем только те из них, которые удовлетворяют неравенствам (11) и (12).

Задача 3 аналогична задаче 2, но рассматривается граница j ₂(X)=0 и оставляемые э.т. должны удовлетворять неравенствам (10) и (12). Такова же и задача 4, в которой исследуются точки на границе j ₃(X)=0.

Следующие три задачи заключаются в исследовании границ, образованных одновременно двумя ограничениями. Так, задача 5 имеет вид

f (X) ® min,

j ₁ (X)=0,

j ₂ (X)=0.

Предполагая, что два уравнения можно разрешить относительно двух переменных, и подставив выражения этих переменных в f (X), сведем задачу 5 к задаче на безусловный экстремум размерности n -2. Если она разрешима, получим соответствующие э.т., которые следует "просеять" через условие (3.12). Оставшиеся точки добавляем к ранее выделенным.

Задачи 6 и 7 аналогичны задаче 5, но границы порождаются другими парами условий. Еще одна граница образуется пересечением границ всех трех условий. Для ее исследования решаем задачу 8:

f (X)® min,

j₁ (X)=0, j₂ (X)=0,

j₃ (X)=0.

Если три представленных уравнения разрешимы относительно трех переменных, то задача 8 сводится к задаче на безусловный экстремум размерности n -3. Так как при этом использовались все условия исходной задачи, то проверять найденные э.т. на принадлежность допустимой области не надо. Последняя задача 9 состоит в определении глобального минимума. Для этого вычисляются значения функции f (X) во всех точках, выявленных в задачах 1-8, и из них выбирается наименьшее.

Рассмотренный пример высвечивает все проблемы, возникающие при решении задачи математического программирования методом классического анализа. На каждом этапе решения нам приходилось делать оговорки типа "если", "предполагая". Невыполнение какой-либо одной из них создает неразрешимую ситуацию. Но и при возможности реализации приведенной схемы трудоемкость решения задачи весьма велика.

ЗАКЛЮЧЕНИЕ

Кратко подводятся итоги занятия, при этом обращается внимание студентов на цели и содержание дисциплины.

Дать задание на самостоятельную работу:

ó с целью более глубокого освоения материала повторить и более подробно изучить линейную оптимизацию. Литература: [3] с. 37…51, конспект лекций,

При необходимости ответить на возникшие вопросы.

Старший преподаватель кафедры АС и ПО И.Денисова

Дата добавления: 2014-01-07