
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нелинейных элементов
|
|
|
|
I.4. Определение характеристик соединений
Нелинейные элементы в системах управления могут быть соединены: параллельно, последовательно или в виде обратной связи. Для упрощения анализа такие соединения обычно заменяются одним нелинейным звеном. Характеристики этого эквивалентного звена определяются по характеристикам исходных элементов в зависимости от типа соединения.
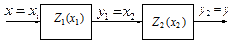 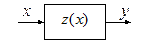 а б
Рис. I.19
а б
Рис. I.19
|
Последовательное соединение. Схема этого соединения показана на рис. I.19, а. На рис. 19,б показана эквивалентная этому соединению нелинейность. Характеристика соединения определяется выражением
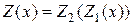 .
.
Графическое построение результирующей нелинейности  при последовательном соединении (рис. I.19) показано на рис. I.20.
при последовательном соединении (рис. I.19) показано на рис. I.20.
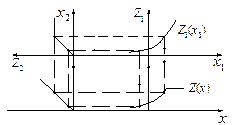 Рис. I.20
Рис. I.20
|
Параллельное соединение. Схема этого соединения показана на рис. I.21. Характеристика соединения определяется выражением
 Рис. I.21
Рис. I.21
|
Построение характеристики параллельного соединения, очевидно, выполняется суммированием характеристик 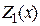 и
и 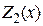 вдоль оси ординат и не составляет каких-либо проблем. Поэтому здесь не рассматривается.
вдоль оси ординат и не составляет каких-либо проблем. Поэтому здесь не рассматривается.
Соединение в виде обратной связи. Схема этого соединения показана на рис. I.22.
Для определения характеристики этого соединения запишем в соответствии со структурной схемой следующие уравнения замыкания:
 Рис. I.22
Рис. I.22
|
а)  ,
,
б) 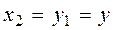 .
.
Ведем функцию, обратную зависимости 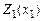 , и обозначим её
, и обозначим её  . Из уравнения а) для случая отрицательной обратной связи можно записать
. Из уравнения а) для случая отрицательной обратной связи можно записать
 .
.
В силу уравнения замыкания б) переменная 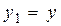 , а
, а  . Поэтому из предыдущего равенства выводим
. Поэтому из предыдущего равенства выводим
 .
.
Отсюда следует, что для получения обратной зависимости 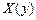 необходимо сложить (при отрицательной обратной связи) вдоль горизонтальной оси величины
необходимо сложить (при отрицательной обратной связи) вдоль горизонтальной оси величины  и
и  соответствующие некоторым значениям x, которые откладываются вдоль вертикальной оси.
соответствующие некоторым значениям x, которые откладываются вдоль вертикальной оси.
Для получения же искомой характеристики  необходимо это же построение выполнить для характеристик
необходимо это же построение выполнить для характеристик 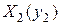 и
и  , также складывая их вдоль горизонтальной оси при некоторых значениях y.
, также складывая их вдоль горизонтальной оси при некоторых значениях y.
  Рис. I.23 Рис. I.24
Рис. I.23 Рис. I.24
|
Например, если характеристики  и
и 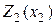 имеют вид, показанный на рис. I.23 и рис. I.24, то необходимые построения при отрицательной обратной связи выполняются так, как показано на рис. I.25.
имеют вид, показанный на рис. I.23 и рис. I.24, то необходимые построения при отрицательной обратной связи выполняются так, как показано на рис. I.25.
 Рис. I.25
Рис. I.25
|
При положительной обратной связи построение характеристики рассматриваемого соединения отличается от приведенного на рис. I.25 лишь тем, что из 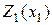 необходимо вычесть
необходимо вычесть 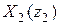 также при некоторых значениях
также при некоторых значениях 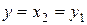 .
.
Рассмотренные преобразования нелинейностей удобно выполнять с помощью ПЭВМ. Эти преобразования необходимы для упрощения структурных схем нелинейных систем, в частности, при исследовании установившихся режимов этих систем.
Отметим, что уравнения установившихся режимов получают из уравнений систем (I.1) полагая в них 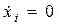 Уравнения установившихся режимов систем управления, как правило, являются нелинейными. Из них обычно получают статические характеристики, которые определяют зависимости между различными величинами системы в установившемся режиме.
Уравнения установившихся режимов систем управления, как правило, являются нелинейными. Из них обычно получают статические характеристики, которые определяют зависимости между различными величинами системы в установившемся режиме.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 445; Нарушение авторских прав?; Мы поможем в написании вашей работы!