
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
I.3. Общие свойства нелинейностей. Типовые звенья
|
|
|
|
Общее обозначение нелинейных элементов или звеньев показано на рис. I.6. Здесь  – характеристика нелинейного звена, т.е. зависимость его выходного сигнала
– характеристика нелинейного звена, т.е. зависимость его выходного сигнала  от входного
от входного  при очень медленном изменении последнего.
при очень медленном изменении последнего.
 Рис. I.6
Рис. I.6
|
В общем случае характеристики нелинейных звеньев могут быть:
1. Симметричными. В этом случае выполняется либо условие
 , либо условие
, либо условие  . В первом случае характеристики называются нечётными, а во втором – четными.
. В первом случае характеристики называются нечётными, а во втором – четными.
2. Непрерывными. В этом случае в любой точке 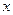 нелинейной характеристики предел справа равен пределу слева, т.е.
нелинейной характеристики предел справа равен пределу слева, т.е. 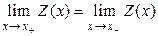 .
.
3. Разрывными. В этом случае в некоторых точках нелинейности предел справа не равен пределу слева, т. е.  .
.
4. Однозначными или многозначными. В случае двузначной характеристики говорят, что нелинейный элемент обладает гистерезисом. В общем случае нелинейные звенья с неоднозначными характеристиками ведут к более существенному изменению свойств системы.
5. Обычно , но не всегда. Например, для петли гистерезиса (см. рис. I.2)
, но не всегда. Например, для петли гистерезиса (см. рис. I.2)  .
.
6. Многие нелинейности обладают насыщением.Это свойство характеризуется тем, что при больших значениях модуля входной величины модуль выходной величины нелинейного звена достигает максимального значения C, а затем перестает изменяться, т.е. остается постоянным, несмотря на увеличение входной величины. Нелинейная характеристика с насыщением (сплошная линия) показана на рис. I.7.
 Рис. I.7
Рис. I.7
|
Аналитическое описание нелинейности с насыщением имеет вид
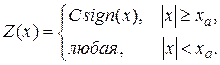
Насыщением обладают все реальные элементы. В частности, статическая характеристика вход-выход всех электронных усилителей имеет насыщение.
7. Важной характеристикой нелинейностей является зона нечувствительности. Характеристика с зоной нечувствительности (сплошная линия) показана на рис. I.8. Здесь интервал значений  от
от  до
до  является зоной нечувствительности, так как в этом диапазоне изменения величины
является зоной нечувствительности, так как в этом диапазоне изменения величины  выходная величина y звена равна нулю.
выходная величина y звена равна нулю.
 Рис. I.8.
Рис. I.8.
|
Характеристики с зоной нечувствительности могут быть описаны выражением вида:

К примеру, зону нечувствительности имеет нелинейная зависимость скорости холостого хода двигателя постоянного тока от напряжения на якоре при постоянном напряжении на обмотке возбуждения. В этом случае «величина зоны нечувствительности», т.е. величина  , равна напряжению трогания, которое обусловлено моментом трения в подшипниках якоря двигателя.
, равна напряжению трогания, которое обусловлено моментом трения в подшипниках якоря двигателя.
Характеристики с зоной нечувствительности – одни из самых распространенных нелинейностей. Характеристикой такого типа обладает большинство датчиков. Например, проволочный потенциометрический датчик (см. рис. I.3) имеет характеристику, показанную на рис. I.9. Здесь зона нечувствительности –  обусловлена толщиной витка обмотки потенциометрического датчика.
обусловлена толщиной витка обмотки потенциометрического датчика.
 Рис. I.9
Рис. I.9
 Рис. I.10
Рис. I.10
|
Чувствительные элементы, питаемые переменным током, тоже имеют зону нечувствительности, которая обусловлена влиянием высших гармоник.
В этом случае характеристика обычно имеет вид, показанный на рис. I.10. Когда входная величина  , находиться внутри зоны нечувствительности, выходная переменная датчика является случайной величиной, среднее значение которой равно нулю
, находиться внутри зоны нечувствительности, выходная переменная датчика является случайной величиной, среднее значение которой равно нулю
Лишь за пределами зоны нечувствительности шириной 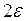 , выходная переменная датчика начинает изменяться определенным образом.
, выходная переменная датчика начинает изменяться определенным образом.
Отметим, что именно зоны нечувствительности элементов в первую очередь определяют статическую точность системы.
Рассмотрим некоторые типовые нелинейные звенья (нелинейности) и их характеристики.
 Рис. I.11
Рис. I.11
|
Идеальное реле. Данная характеристика показана на рис. I.11 сплошными линиями.
При 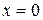 эта характеристика не определена. Аналитическое выражение этой характеристики имеет вид
эта характеристика не определена. Аналитическое выражение этой характеристики имеет вид
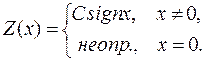
 Рис. I.12
Рис. I.12
|
Данной характеристикой описывается, например, поляризованное реле, схема которого показана на рис. I.12. При подаче на обмотку такого реле напряжения одной полярности магнитный поток и сила притяжения якоря к магниту уменьшаются, и замыкается верхняя пара контактов. В цепи нагрузки формируется напряжение одного знака. При подаче на обмотку реле напряжения противоположной полярности магнитный поток наоборот увеличится и замкнется нижняя пара контактов. В результате на нагрузку будет подано напряжение другого знака.
Такие элементы применяются при реализации оптимального управления. Знаковая функция является идеализацией реальных характеристик, одна из которых показана на рис. I.11 пунктирной линией.
 Рис. I.13
Рис. I.13
|
Трехпозиционное реле. Эта характеристика имеет вид, показанный на рис. I.13.
Как видно, она является разрывной, симметричной, нечетной, однозначной. Аналитическое описание этой характеристики:
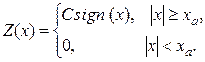
 Рис. I.14
Рис. I.14
|
Здесь  – зона нечувствительности данного реле.
– зона нечувствительности данного реле.
При  эта характеристика переходит в нелинейность – идеальное реле. Характеристику, показанную на рис. I.13, имеет схема, приведенная на рис. I.14, если принять, что ток отпускания обоих реле равен их току срабатывания (на самом деле, ток отпускания всегда меньше тока срабатывания, но не намного).
эта характеристика переходит в нелинейность – идеальное реле. Характеристику, показанную на рис. I.13, имеет схема, приведенная на рис. I.14, если принять, что ток отпускания обоих реле равен их току срабатывания (на самом деле, ток отпускания всегда меньше тока срабатывания, но не намного).
Входная переменная x представлена здесь напряжением 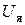 . Зона нечувствительности
. Зона нечувствительности  определяется током срабатывания, а
определяется током срабатывания, а 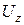 равно E. Если из этой схемы удалить нормально замкнутые контакты
равно E. Если из этой схемы удалить нормально замкнутые контакты  то данная схема будет описывать релейную двухпозиционную характеристику, так как значение
то данная схема будет описывать релейную двухпозиционную характеристику, так как значение 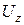 при
при  не будет определяться этой схемой.
не будет определяться этой схемой.
Трехпозиционное реле с гистерезисом. Эта характеристика приведена на рис. I.15. Здесь интервал значений  от –
от – до
до  является зоной нечувствительности; интервалы от
является зоной нечувствительности; интервалы от  до –
до –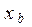 и от
и от  до
до  являются областью неоднозначности (областью гистерезиса).
являются областью неоднозначности (областью гистерезиса).
При аналитическом описании этой характеристики необходимо учитывать не только значения величины  , но и скорость
, но и скорость 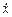 её изменения. В результате получим следующее выражение:
её изменения. В результате получим следующее выражение:
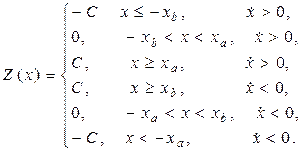
Примером нелинейного элемента, который может быть описан данной характеристикой, является показанный на рис. I.14 релейный элемент, если ток отпускания реле считать не равным току срабатывания. Для этой схемы величина  (см. рис. I.15) определяется током срабатывания, а величина
(см. рис. I.15) определяется током срабатывания, а величина  – током отпускания реле.
– током отпускания реле.
 Рис. I.15
Рис. I.15
|
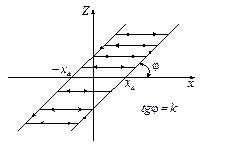 Рис. I.16
Рис. I.16
|
Люфт. Эта характеристика обычно присуща механическим передачам и обусловлена зазором (люфтом) в сочленениях элементов. Она приведена на рис. I.16. Аналитическое описание её практически не используется, т. к. является очень сложным и непрактичным. Обычно оно заменяется словесным, например, следующим.
Если величина  возрастает, то зависимость
возрастает, то зависимость  соответствует прямой, смещенной вправо от нуля на величину
соответствует прямой, смещенной вправо от нуля на величину  . Если же величина
. Если же величина  убывает, то зависимость
убывает, то зависимость  соответствует прямой, смещенной влево от нуля на величину
соответствует прямой, смещенной влево от нуля на величину  . При изменении знака скорости величины x вначале будет наблюдаться холостой ход, то есть выходная величина
. При изменении знака скорости величины x вначале будет наблюдаться холостой ход, то есть выходная величина  меняться не будет в течение времени, пока x не изменится на величину большую 2
меняться не будет в течение времени, пока x не изменится на величину большую 2 .
.
 Рис. I.17
Рис. I.17
|
Характеристика люфт является неоднозначной и вносит некоторое запаздывание в работу систем управления. Она весьма отрицательно сказывается на свойствах динамических систем. Помимо уменьшения точности она может приводить к возникновению незатухающих колебаний в системе, амплитуда которых может значительно превышать «люфт». Коэффициент передачи звена типа люфт, в линейном режиме равен тангенсу угла  , как показано на рис. I.16.
, как показано на рис. I.16.
На рис. I.17 показана причина образования этой нелинейности в шарнирном соединении. Хорошо видно, что пока вилка, поворачиваясь вместе с ведущим валом на угол 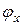 , не касается пальца, соединенного с ведомым валом, последний неподвижен, а после касания – поворачивается вместе с ведущим валом на угол
, не касается пальца, соединенного с ведомым валом, последний неподвижен, а после касания – поворачивается вместе с ведущим валом на угол  .
.
При изменении направления вращения ведущего вала ведомый вал сначала останавливается, так как вилка отходит от пальца, а затем, после того как люфт (ширина вилки) будет выбран, ведомый вал начинает вращаться вместе с ведущим.
Кусочно-ломаная характеристика. Эта характеристика приведена на рис. I.18. Как видно, она состоит из ряда линейных участков, угол наклона которых различный. Этой характеристикой обычно описывают различные исполнительные механизмы, тиристорные или магнитные усилители и т.д.
 Рис. I.18
Рис. I.18
|
Реальные элементы систем часто имеют характеристики, являющиеся комбинацией указанных типов нелинейностей.
Если реальная нелинейная характеристика имеет один линейный участок, то соответствующая ей типовая характеристика имеет линейный участок, проходящий под наклоном  . Это связанно с тем, что значение коэффициента передачи реальной нелинейной характеристики обычно относят к линейной части системы.
. Это связанно с тем, что значение коэффициента передачи реальной нелинейной характеристики обычно относят к линейной части системы.
Все однозначные нелинейности фактически являются безынерционными, так как имеющиеся у реальных элементов постоянные времени (например, электромагнитная постоянная обмотки реле) также относят к линейным элементам нелинейных систем. Однако, несмотря на это, многозначные нелинейные характеристики (например, с гистерезисом), вносят дополнительное запаздывание, что приводит к сдвигу фазы гармонических составляющих в разложении выходного сигнала таких элементов в ряд Фурье. Поэтому нелинейные звенья с неоднозначными статическими характеристиками фактически являются динамическими нелинейными звеньями.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 4337; Нарушение авторских прав?; Мы поможем в написании вашей работы!