Построение движения точки по заданному ее ускорению

Пусть теперь известно ускорение 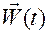в любой момент времени 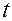из промежутка, на котором должно быть определено движение.

Движение связано с ускорением следующим соотношением:

. (1.1.6)

Если учесть, что скорость 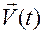связана с ускорением 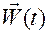(по определению) соотношением

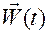, (1.1.7)

то из (1.1.7) можем определить скорость 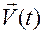по известному вектору .

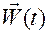Для этого воспользуемся формулой (1.1.5)

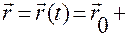
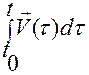, (1.1.5)

в которой 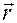, , 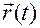, 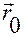заменим соответственно на , , , ;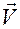

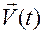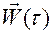обозначает вектор скорости, которую имеет материальная точка в момент времени .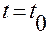

Получим

. (1.1.8)

Учитывая связь (1.1.3):

(1.1.3)

скорости 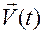с движением 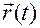, подставим найденную функцию 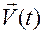в (1.1.5):

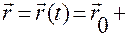
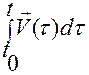. (1.1.5)

В результате получим вектор-функцию 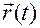, определяющую такое движение материальной точки, при котором она имеет ускорение, совпадающее в каждый момент времени 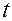с заданным ускорением :

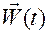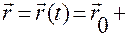
. (1.1.9)

На этом движении материальная точка в момент времени 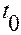проходит через положение 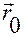и имеет в нем скорость .

Из (1.1.9) следует, что для однозначного построения движения материальной точки по ускорению 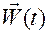требуется задать не только положение 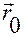в момент 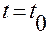, но и скорость .

Примечание 1

Если известна скорость 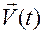, то, как следует из сказанного, движение определяется из уравнения (1.1.3):

. (1.1.3)

посредством вычисления интеграла от вектора скорости.

В уравнение (1.1.3) движение входит через свою производную по времени.

Равенство, в которое входят производные от неизвестной функции, зависящей от одного аргумента, называется обыкновенным дифференциальным уравнением.

Порядком уравнения называют наивысший порядок производной от неизвестной функции, с которым эта функция входит в данное уравнение. При этом сама функция может входить или не входить в уравнение.

Как видим, уравнение (1.1.3)

(1.1.3)

является дифференциальным уравнением первого порядка относительно вектор-функции 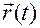, а уравнение (1.1.6):

(1.1.6)

— дифференциальным уравнением второго порядка.

Функция, дифференцируемая в количестве раз, совпадающем с порядком дифференциального уравнения, и обращающая это уравнение в тождество относительно независимой переменной, называется решением данного дифференциального уравнения.

Согласно этому определению, вектор-функция 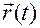, задаваемая формулами (1.1.5)и (1.1.9), является решением уравнения (1.1.3) и (1.1.6), соответственно.

Таким образом, если движение точки определять через скорость или ускорение, то оно строится как решение векторного обыкновенного дифференциального уравнения.

В таких случаях дифференциальное уравнение, решением которого является закон движения материальной точки, называется математической моделью ее движения.

2º. Координатный способ задания движения точки

Дата добавления: 2014-01-07