Определение 2

Годографом вектор-функции 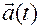называется геометрическое место точек в абсолютном пространстве, образованное концами векторов 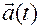, имеющих своим началом точку отсчета .

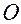Очевидно, годограф вектор-функции 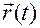, задающей движение, совпадает с траекторией движения точки.

Понятие годографа чаще всего применяется к скорости движения точки (называется годографом скорости) и к ее ускорению (годограф ускорения).

Если известна скорость 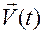материальной точки при всех , то для построения ее годографа:

· необходимо параллельным переносом совместить начало вектора скорости точки 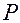с точкой отсчета 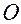в каждый момент времени ;

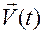· геометрическое место концов построенного таким образом множества векторов при всех будет являться годографом вектора скорости точки .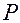

Аналогично строится годограф ускорения 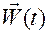этой точки.

Годограф скорости 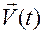в трехмерном пространстве параметрически задается уравнениями

где

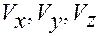— координаты точек годографа скорости,

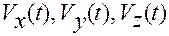— координаты скорости материальной точки в момент времени .

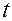Аналогично, для годографа ускорения 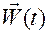параметрические уравнения имеют вид

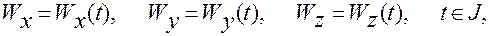
где

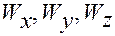— координаты точек годографа ускорения,

— координаты ускорения материальной точки.

3º. Описание естественного способа задания движения

Суть естественного способа задания движения материальной точки такова: задается траектория и закон движения точки по этой траектории.

Математически этот способ задания движения описывается следующими действиями:

– задается регулярная кривая не ниже второй кратности (без особых точек) в естественной параметризации

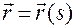; (1.2.5)

– задается закон движения по этой кривой

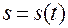, (1.2.6)

где

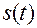— дважды непрерывно дифференцируемая функция, зависящая от .

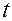От естественного способа легко перейти к векторному способу задания движения точки, т. е. найти прямую связь естественного способа с векторным.

Векторный способ задания движения точки находится подстановкой закона движения (1.2.6) в уравнение траектории (1.2.5). В результате подстановки получим

. (1.2.7)

Соотношение (1.2.7) — это векторный способ задания движения.

Общая схема перехода от векторного способа задания движения к естественному способу (обратная связь) описана ниже в Дополнении 2 к §2 этой главы.

4º. Вычисление скорости и ускорения при естественном способе задания движения

Дата добавления: 2014-01-07