Замечание 2

Если в формуле (1.2.9) окажется, что 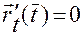при каких-то значениях 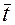, то подбираем новую параметризацию 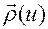, в которой параметр 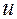связан со временем 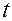соотношением

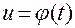, (1.2.11)

допускающим однозначное и дважды непрерывно дифференцируемое обращение .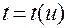

Основное требование к указанной параметризации следующее:

-вектор-функция , определяемая по формуле

(1.2.12)

должна иметь значение

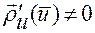при .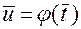

Поскольку траектория движения 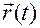является регулярной кривой без особых точек, то такая параметризация 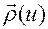существует.

Данное утверждение следует из того, что для регулярных кривых без особых точек всегда существует естественная параметризация 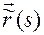. А в естественной параметризации при всех значениях длины дуги 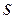выполняется равенство

.

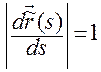После построения параметризации 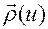траектория с учетом соотношения (1.2.12) будет задаваться равенством

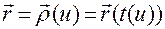(1.2.13)

А тогда функцию 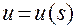находим путем обращения функции 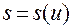, где 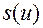имеет следующую зависимость от функции :

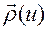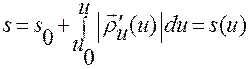. (1.2.14)

Соотношение (1.2.14) выводится по той же схеме, по которой получено (1.2.9):

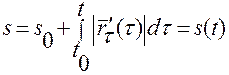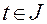, (1.2.9)

Это делается путем замены 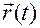на .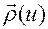

Так как функция 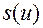, определяемая по формуле (1.2.14), обладает свойством

,

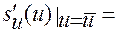
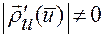то в окрестности точки 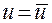, 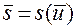она допускает обращение

.

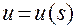Подстановка вместо :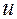

1) функции 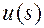в соотношение (1.2.13)

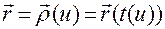, (1.2.13)

2) функции 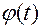из (1.2.11)

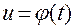, (1.2.11)

в функцию 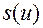, определяемую по формуле (1.2.14)

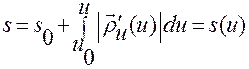, (1.2.14)

дает окончательно естественный способ задания движения:

, .

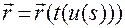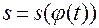Дата добавления: 2014-01-07