Следствие из соотношений Коши

Обобщенный закон Гука

Соотношения Коши

- первое соотношение Коши

В силу малости угла g: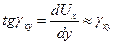, даже при g=30⁰ погрешность составляет около 5%.

Аналогично .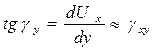

При вычислении деформаций наибольшее значение имеет суммарное изменение угла: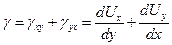

Оно ограничивает применение метода коллокаций (условие совместности деформаций)

Подставляя сюда g,e_х, e_у по закону Гука получим связь:

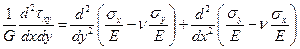
Таким образом выбирать аппроксимации для напряжений произвольным образом нельзя, так как должны выполняться условия совместности деформаций.

Вторая краевая задача теории упругости

Если не нужно выполнять условия закрепления конструкции, то задача называется первой краевой задачей теории упругости.

Если тело закреплено со всех сторон (если заданы перемещения границы), то задача называется второй краевой задачей теории упругости.

Если часть края конструкции закреплена, а другая часть свободна, то задача называется смешанной краевой задачей теории упругости.

Методика решения задач при наличии закреплений:

1. Перемещения задаются в виде аппроксимаций с неизвестными (искомыми) коэффициентами. Например:

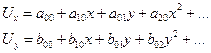
2. Записываются выражения для деформаций:

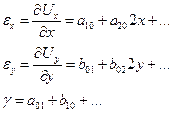
3. Находим выражение для напряжений:

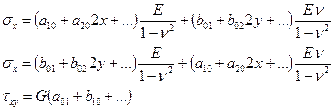
Знаменатель (1-n²) появляется тогда, когда определяем σ_х, σ_у через e_х, e_у.

4. Соотношения пункта 1. подставляются в условия закрепления, а соотношения из пункта 3. в уравнения равновесия. Получается система уравнений, которая содержит искомые коэффициенты, а также функции х,у,х²,у²…

5. Выбирается какой либо метод, который позволяет исключить х,у и их функции из полученной системы.

Задача: растяжение балки-стенки

q_x=2x², p₀=5, n=0

Решение:

Видно что σ_у в нашей задаче равно нулю (σ_у=0), так как n=0, также отсутствуют сдвиги τ_ху=0.

Получаем уравнения равновесия в виде:

для внутреннего элемента

при х=2 – для краевого элемента

Зададим условия закрепления при х=0 U_x=0

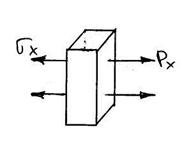
1.

2.

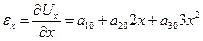
3.

4.

5. Используем метод коллокаций для получения алгебраической системы:

Выберем элементы коллокации

х₁=0

х₂=2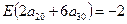

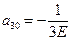
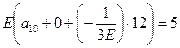
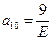
Таким образом:

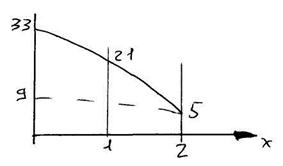
Построим эпюру напряжений по длине.

Недостатки метода коллокаций:

~ Решение сильно зависит от точек коллокации, если брать число искомых коэффициентов не очень большим (2¸3)

Второй вариант точек коллокации:

При х₁=0

Из уравнения равновесия граничного элемента:

Теперь решение принимает вид:

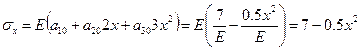
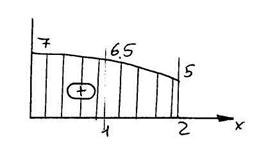
Метод Бубнова-Галеркина

Как и в методе коллокаций решение ищется в виде аппроксимации с неизвестными коэффициентами, то есть:

Аналогично находятся деформации и перемещения: . Напряжения подставляются в уравнения равновесия внутреннего и граничных элементов, перемещения подставляются в условия закрепления. В результате получаем не алгебраические, а функциональные уравнения.

Уравнения равновесия внутреннего элемента:

F(a₀₀, …, х)=-q(x)

Уравнения равновесия граничных элементов:

H (a₀₀,… х)=p(x)

Условия закрепления:

G (a₀₀, …, х)=0

Слева и справа в этих уравнениях функции близки друг к другу, значит и интегралы от них должны быть почти одинаковы

Исходные уравнения можно умножать на любую функцию, от этого равенство не изменится, после этого можно интегрировать еще раз

…

Недостаток метода в том, что ,… выбираются расчетчиком, следовательно решение достаточно субъективно, однако математиками доказано, что, как правило наилучшее приближение к точному решению получается тогда, когда в качестве ,… берутся функции использованные для аппроксимации перемещений.

Рассмотрим пример:

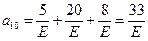
Дата добавления: 2014-01-07