Наличие теоретического закона распределения коэффициента позволяет нам сказать с какой вероятностью возможно определенное значение этого коэффициента

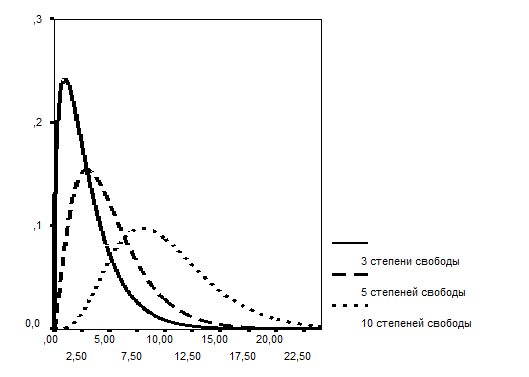
Каково же теоретическое распределение коэффициента χ²? Это теоретическое распределение носит то же название - χ². Таким образом, под одним термином «хи - квадрат» скрываются две совершенно разные сущности – коэффициент, фиксирующий степень расхождения теоретических и эмпирических частот, и закон распределения. На рисунке 2.5 показан график плотности функции распределения χ² с различными степенями свободы.

Рисунок 2.5

Функция плотности распределения χ²

с различным числом степеней свободы.

На рисунке 2.6 показаны графики вероятности того, что случайная величина, распределенная по закону χ², не превзойдет определенное значение.

Вероятность того, что случайная величина,

распределенная по закону χ² не превзойдет значение x.

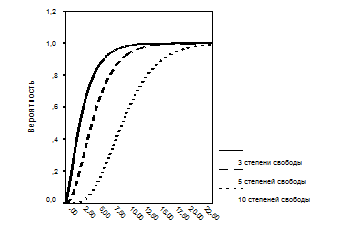
Рисунок 2.6

Если графики рисунка 2.5 представляют скорее теоретический интерес, то графики, изображенные на рисунке 2.6 имеют практический смысл. Например, если мы получили, что при 5 степенях свободы коэффициент χ² для нашей таблицы равен 10, то по графику можно определить, что с вероятностью Р =0,92, при справедливости равенства наблюдаемых и ожидаемых частот, χ² должен был бы быть меньше 10. Следовательно, вероятность того, что при таком значении коэффициента χ² наблюдаемые и ожидаемые частоты равны, составляет P = 1-0,92 = 0,08.

Для понимания предыдущих рассуждений осталось объяснить, что же такое «степени свободы». Значение χ² зависит от 2-х показателей – степени расхождения ожидаемых и наблюдаемых частот в клетках таблицы и от количества самих клеток. Действительно, мы можем получить большую величину χ² если ожидаемые и наблюдаемые частоты сильно расходятся, но можем и в ситуации, когда расхождения этих частот маленькие, но самих слагаемых много. Очевидно, что это два совершенно разных случая. В первом у нас, по всей видимости, имеет место случай неподтверждения модели независимости переменных. Во втором, скорее наоборот. Таким образом, одно и то же значение коэффициента χ² возможно в двух противоположных ситуациях. Причина тому, просто-напросто, в разном количестве клеток в таблице. Следовательно, когда мы говорим о величине χ², необходимо говорить и о числе клеток. Эта характеристика и фиксируется показателем «число степеней свободы». Вычисляется число степеней свободы по формуле: N=(r-1)(c-1), где N - число степеней свободы, r – число строк в таблице, c – число колонок.

Таким образом, если вернуться к разбору вопроса о наличии связи между переменными Q10 и Q12 в таблице 2.5, мы получаем, что для этой таблицы коэффициент хи-квадрат равен 195 при 9 степенях свободы. На рисунке 2.6 нет графика вероятности различных значений для 9 степеней свободы, но в таблице распределений χ² можно найти, что вероятность такого значения крайне мала (P <0,0001). Следовательно, можно утверждать, что справедливость гипотезы о равенстве наблюдаемых и ожидаемых частот (то есть гипотезы о независимости этих переменных) подтверждается данными исследования с вероятностью P <0,0001. Как результат мы можем говорить, что с вероятность P >0,999 справедлива гипотеза об отсутствии независимости между Q10 и Q12, то есть об их взаимосвязи.

Ограничения использования коэффициента хи-квадрат.

Доказано, что коэффициент хи-квадрат будет иметь теоретическое распределение хи-квадрат только в случае, когда ожидаемые частоты в таблице имеют значения 5 и более. Это не значит, что если в таблице есть ожидаемые частоты меньше 5, то нельзя пользоваться формулой (2.1) для вычисления коэффициента хи-квадрат. Формулой пользоваться можно, однако, это становится вполне бессмысленным.

Это ограничение является достаточно болезненным при анализе социологических данных. Действительно, даже в таблице 2.5, не смотря на большое число опрошенных, мы видим, что в 3-х клетках из 16 ожидаемые частоты имеют значения меньше 5. При этом само ограничение выглядит несколько странным. Действительно, если у нас есть таблица со 100 клетками, и, только в одной клетке ожидаемая частота меньше 5, то неужели распределение будет настолько отличаться от теоретического что нельзя пользоваться таблицами?

Существует эмпирическое правило, что если в таблице не больше 20% клеток, в которых ожидаемая частота меньше 5, и нет клеток, в которых ожидаемая частота меньше 1, то реальное распределение коэффициента хи-квадрат достаточно хорошо описывается теоретическим распределением хи-квадрат [1]. В другой работе указывается, что для использования теоретического распределения хи-квадрат достаточно, чтобы ожидаемые частоты были больше 3 [2].

Такая размытость в рекомендациях позволяет придти к общему выводу: для корректного использования коэффициента хи-квадрат необходимо стремиться к тому, чтобы клеток с маленькими ожидаемыми частотами было как можно меньше.

Дата добавления: 2014-01-07