Коэффициент корреляции Пирсона

В том случае, когда обе анализируемые переменные измерены по метрическим шкалам (интервальным, либо абсолютным) у нас появляется дополнительная возможность измерения степени взаимосвязи между этими переменными – это коэффициент корреляции Пирсона. Формула, для вычисления этого коэффициента корреляции достаточно проста (2.9).

где 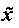и - средние значения переменных x и y, соответственно;

S_x и S_y – стандартные отклонения переменных x и y;

N – количество наблюдений.

Из формулы (2.9) следует, что коэффициент r фиксирует степень того, на сколько переменные x и y одновременно отклоняются от своих средних значений. Таким образом, в отличие от ранговых коэффициентов корреляции, которые замеряют монотонный характер связи между переменными, коэффициент корреляции Пирсона учитывают более узкий характер монотонности – линейность. В том случае, когда между переменными есть строгая линейная зависимость значение коэффициента корреляции Пирсона будет равно +1 в случае положительной связи и -1 в случае отрицательной связи..

Нулевое значение коэффициента Пирсона, строго говоря, свидетельствует только об отсутствии линейной зависимости. Это, свою очередь, может говорить и об отсутствии вообще какой-либо зависимости, и о том, что зависимость есть, но она носит нелинейный характер. Установить с помощью данного коэффициента, с какой из этих ситуаций мы имеем дело в конкретном случае нельзя.