Коэффицент ранговой корреляции Кендалла

Коэффицент ранговой корреляции Спирмена

Пусть выборка наблюдений двух переменных Х и Y. Упорядочим элементы по возрастанию и найдем ранг каждого элемента 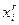. Аналогично определим ранги для переменной Y.

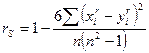
k- число инверсий в ряду рангов второй переменной, при условии, что ранги первой переменной упорядочены.

В случае совпадающих рангов для расчета ранговых коэффицентов используются скорректированные формулы.

Пример.

X	68.8	63.3	75.5	67.2	71.3	72.8	76.5	63.5	69.9	71.4
Y

Перепишем таблицу, упорядочив ее по верхней строке

X	63,3	63,5	67,2	68,8	69,9	71,3	71,4	72,8	75,5	76,5
Y

Определим ранги для Y

ранг
Y

Получим таблицу пар рангов:

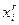
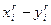
			-2	-4				-2

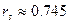- коэффициент Спирмана

Найдем коэффициент Кендалла. Найдем число инверсий (нарушений порядка) в последовательности . Число 5 образует две инверсии, так как стоит перед числами 3 и 4. 8 – образует 4 инверсии с числами 3, 4 и 6. 7-образует одну инверсию, 10-две. Число инверсий равно 9.

Отличие ранговых коэффициентов корреляции от коэффициентов связи, основанных на χ², в том, что фиксируют не только наличие, либо отсутствие связи, но и, в случае наличия связи, ее направление. Это, несомненно, является достоинством данных коэффициентов, но, в определенных случаях может являться и их недостатком. Дело в том, что ранговые коэффициенты корреляции фиксируют только однонаправленные, монотонные формы зависимости, вроде тех, которые изображены на рисунке 2.7

Что произойдет, если зависимость между переменными не имеет однонаправленной связи, как, например, зависимости, изображенные на рисунке 2.8? Оказывается, что в ситуации такого рода форм зависимостей ранговые коэффициенты связи оказываются неэффективными.

Действительно, если может оказаться, что для части респондентов, например тех, кто имеет малые значения переменной Х (график 1 рисунка 2.12) значение рангового коэффициента связи будут отрицательные, а для тех респондентов, которые имеют большие значения переменной Х ранговый коэффициент будет положительный, то общее значение рангового коэффициента может оказать равным 0. И это при том, что, как показывает график, связь между переменными явно есть.

Таким образом, тот факт, что значение рангового коэффициента корреляции равно 0 не говорит об отсутствии связи, а говорит лишь об отсутствии монотонной связи.

Если при изучении взаимосвязи двух порядковых переменных мы получили нулевое значение ранговой корреляции, то как можно проверить с какой из ситуаций мы имеем дело: между переменными вообще нет зависимости, либо между переменными нет монотонной зависимости? Ответ достаточно прост: следует посчитать, скажем, коэффициент χ². Если этот коэффициент покажет наличие связи при нулевом значении коэффициента γ, то, очевидно, что мы имеем дело с наличием немонотонной связи между переменными.

Рисунок 2.7

Примеры монотонных зависимостей между переменными

Рисунок 2.8

Примеры немонотонных зависимостей между переменными

Дата добавления: 2014-01-07