Вводная часть. IV. Учебно-материальное обеспечение

V. Текст лекции

IV. Учебно-материальное обеспечение

I. Цели занятия

Тема 3.2. Статически определимые и неопределимые стержневые системы.

СМК-УМК 4.4.2-30-12

Методическая разработка для проведения лекции

по учебной дисциплине «Прикладная механика»

Раздел 3. Сопротивление материалов

Лекция 3.2.1. Статически определимые и неопределимые стержневые системы

Обсуждена на заседании кафедры

(предметно-методической комиссии)

Протокол № _______

«____» _____________ 2012 г.

Санкт-Петербург

1. Ознакомить обучающихся со статически неопределимых стержневых систем, а также изложить методику устранения статической неопределимости при решении практических задач.

2. Прививать обучающимся теоретические основы и навыки, необходимые для решения практических задач.Развивать умение классифицировать факты, делать обобщения и выводы.

3. Воспитывать у обучающихся стремление к углубленному освоению материала по теме занятия, осуществлять связь, между изучаемой дисциплиной и становления обучающихся, как инженеров государственной противопожарной службы.

II. Расчёт учебного времени

Содержание и порядок проведения занятий

Время, мин.

ВВОДНАЯ ЧАСТЬ: принять доклад о готовности группы к занятиям; проверить наличие обучающихся, внешний вид, готовность к занятиям. Объявить тему, цели и учебные вопросы занятия. Подчеркнуть актуальность и значимость темы для дальнейшей практической деятельности обучающихся.   ОСНОВНАЯ ЧАСТЬ Учебные вопросы 1. Расчет статически определимых стержневых систем. 2. Расчет статически неопределимых стержневых систем. 3. Метод сил. Метод сравнения деформаций.   ЗАКЛЮЧИТЕЛЬНАЯ ЧАСТЬ: напомнить тему, цели занятий, ответить на поставленные вопросы, дать задание на самостоятельную работу, самоподготовку; выдать план проведения всех видов занятий

5 минут     80 минут   20 минут 30 минут 30 минут   5 минут

III. Литература

1. Степин П.А. Сопротивление материалов. Учебник для немашиностртельных специальностей вузов. Изд. 8. - М.: Высшая школа. 2000. - 367 с.

2. Феодосьев В.И. Сопротивление материалов. - М.: Наука, 2001.

3. Кочетов В.Т., Кочетов М.В., Павленко А.Д. Учебное пособие. Сопротивление материалов. – СПб: БХВ – Петербург, 2004.

1. Технические средства обучения: мультимедийный проектор, компьютер.

2. Слайды:

· Название темы.

· Учебные вопросы.

· Рекомендуемая литература.

· Далее по вопросам лекции

Принять доклад о готовности группы к занятиям; проверить наличие обучающихся, внешний вид, готовность к занятиям. Объявить тему, цели и учебные вопросы занятия. Подчеркнуть актуальность и значимость темы для дальнейшей практической деятельности обучающихся.

Вопрос 1. Расчёт статически определимых стержневых систем.

Под стержневой системой в широком смысле слова понимается всякая конструкция, состоящая из элементов, имеющих форму стержня. Если элементы конструкции работают в основном на растяжение или сжатие, то стержневая система называется фермой (рис.1). Ферма состоит из прямых стержней, образующих треугольники. Для фермы характерно приложение внешних сил в узлах.

Рис. 1

Если элементы стержневой системы работают в основном на изгиб или кручение, то система называется рамой.

Рис. 2

Особую, наиболее простую для исследования группу стержневых систем составляют плоские системы. У плоской рамы или фермы оси всех составляющих элементов расположены в одной плоскости, которая одновременно является главной плоскостью сечений. В этой же плоскости действуют все внешние силы, включая и реакции опор (см. рис. 2, а).

Наряду с плоскими имеются так называемые плоскопространственные системы. Для такого рода систем оси составляющих элементов в недеформированном состоянии располагаются, как и для плоских систем, в одной плоскости. Внешние же силовые факторы действуют в плоскостях, перпендикулярных этой плоскости (см. рис. 2, б). Стержневые системы, не относящиеся к двум указанным классам, называются пространственными (см. рис. 2, в).

Рамы и фермы принято разделять на статически определимые и статически неопределимые. Под статически определимой понимается такая система, для которой все реакции опор могут быть определены при помощи уравнений равновесия, а затем при найденных опорных реакциях методом сечений могут быть найдены также и внутренние силовые факторы в любом поперечном сечении.

Расчёт статически определимых стержневых систем (последовательность)

а) условие статической определимости:

m = 2n – 3

где:

m – количество стержней;

n – количество узлов;

б) определение реакций опор от заданных внешних нагрузок;

в) выполнение проверки вычислений реакций опор;

г) определение усилий во всех стержнях фермы методом вырезания

узлов

Расчётная схема фермы

Выбираем и проводим оси координат.

m = 2n – 3

7 = 2·5 – 3

где m – количество стержней (m = 7);

n – количество узлов (n = 5);

7 = 7, следовательно, заданная ферма статически определима.

1). Вычисляем реакции опор от заданных внешних нагрузок.

Мысленно отбрасываем опоры и заменяем их реакциями (условно вычерчиваем реакции опор на той же расчётной схеме). Составляем три уравнения равновесия:

S Р (х) = 0 R_В^х + Р₁ – R_А^х = 0;

S Р (у) = 0 R_В^у – Р₂ = 0;

S М(В) = 0 R_А^х · 2 L tgα – Р₁ · L tgα – Р₂ · 2 L = 0;

Решая систему этих трёх уравнений с тремя неизвестными, определяем реакции опор.

R_А^х = (Р₁ · L tgα + Р₂ · 2 L) / 2 L tgα

R_В^х = – Р₁ + R_А^х

2). Производим проверку вычисления реакций опор.

S М(А) = 0 R_В^х · 2 L tgα + Р₁ · L tgα – Р₂ · 2 L = 0

Подставляем в это выражение полученные числовые значения реакций опор, получаем:

0 = 0

Следовательно, реакции опор вычислены верно!

3). Определяем усилия во всех стержнях методом вырезания узлов.

Вычисления усилий в стержнях фермы начинаем с узла, в котором сходится не более двух стержней, усилия внутри которых неизвестны. В данной ферме это узлы «В» и «Е». Рассмотрим узел «В».

Узел «В»

(определяем усилия в стержнях 1 и 4)

1) Мысленно вырезаем узел «В», заменяя действие отброшенной части фермы усилиями в стержнях 1 и 4. Усилия в них направляем от узла.

2) Вычерчиваем узел с приложенными к нему внешними нагрузками, проводим оси координат.

Поскольку рассматриваемый узел находится в равновесии, составляем два уравнения равновесия (по количеству неизвестных):

S Р (х) = 0 S₄ · cosα + R_В^х = 0 (1)

S Р (у) = 0 S₁ + R_В^у + S₄ · sin α = 0 (2)

Из (1) уравнения вычисляем S₄, из (2) уравнения вычисляем S₁:

Узел «А»

(определяем усилия в стержнях 2 и 3)

S Р (х) = 0 – R_А^х + S₃ · cosα + S₂ = 0 (3)

S Р (у) = 0 – S₁ – S₃ · sinα = 0 (4)

Из (3) уравнения вычисляем S₂, из (4) уравнения вычисляем S₃:

Узел «С»

(определяем усилия в стержнях 5 и 6)

S Р (х) = 0 S₆ = S₂

S Р (у) = 0 S₅ = 0;

Этот узел относится к лемме о нулевых стержнях.

Узел «Е»

(определяем усилие в стержне 7)

S Р (х) = 0 – S₆ – S₇ cosα = 0 (5)

Для данного узла достаточно одного уравнения равновесия (5), из которого определяем S₇:

Узел «D»

(проверочный)

S Р(х) = 0 Р₁ + S₇ · cosα – S₃ · cosα – S₄ · cosα = 0

Подставляем найденные значения усилий в стержнях и получим,

что 0 = 0.

Следовательно, усилия в стержнях найдены верно!

Вопрос 2. Расчёт статически неопределимых стержневых систем

1). Связи, накладываемые на систему. Степень статической неопределимости.

Под статически неопределимой системой имеется в виду такая, для которой определение внешних реакций и всех внутренних силовых факторов не может быть произведено при помощи метода сечений и уравнений равновесия.

Разность между числом неизвестных (реакций опор и внутренних силовых факторов) и числом независимых уравнений статики, которые могут быть составлены для рассматриваемой системы, носит название степени, или числа статической неопределимости. В зависимости от этого числа системы разделяют на один, два, три,..., п раз статически неопределимые. Иногда говорят, что степень статической неопределимости равна числу дополнительных связей, наложенных на систему. Остановимся на этом вопросе подробнее.

Положение жесткого тела в пространстве определяется шестью независимыми координатами, иначе говоря, жесткий стержень обладает шестью степенями свободы. На него могут быть наложены связи, т.е. ограничения, обусловливающие его определенное положение в пространстве. Наиболее простыми связями являются такие, при которых полностью исключается то или иное обобщенное перемещение для некоторых сечений. Наложение одной связи снимает одну степень свободы. Следовательно, если на свободный жесткий стержень наложено шесть связей, то положение его в пространстве будет, за некоторыми исключениями, определено полностью, и система из механизма, обладающего шестью степенями свободы, превращается в кинематически неизменяемую систему. То число связей, при котором достигается кинематическая неизменяемость, носит название необходимого числа связей. Всякую связь, наложенную сверх необходимых, называют дополнительной. Число дополнительных связей равно степени статической неопределимости системы.

Связи в рамах и стержневых системах делят обычно на связи внешние и связи внутренние, или взаимные. Под внешними связями понимаются условия, накладываемые на абсолютные перемещения некоторых точек системы. Если, например, на левый конец бруса (рис. 3, а) наложено условие, запрещающее вертикальное перемещение, говорят, что в этой точке имеется одна внешняя связь. Условно ее изображают в виде двух шарниров или катка. Если запрещено как вертикальное, так и горизонтальное смещение, говорят, что наложены две внешние связи (рис. 3, б). Заделка в плоской системе дает три внешние связи (рис. 3, в).

Рис. 3

Внешние связи часто, как уже упоминалось, делят на необходимые и дополнительные. Например, на рис. 4 показана плоская рама, имеющая в случае а три, а в случае б- пять внешних связей. Для того чтобы определить положение рамы в плоскости как жесткого целого, необходимо наложение трех связей. Следовательно, в случае а рама имеет необходимые внешние связи, а случае б, кроме того, две дополнительные внешние связи.

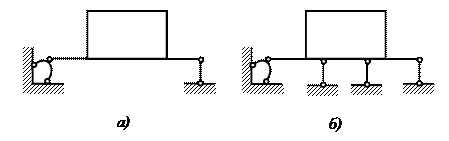
Рис. 4

Под внутренними, или взаимными, связями понимаются ограничения, накладываемые на взаимные смещения элементов рамы. Здесь также можно говорить как о необходимых, так и о дополнительных связях. Например, плоская рама, показанная на рис.5 а, имеет необходимое количество как внешних, так и внутренних связей между элементами.

А

Рис. 5

Это - кинематически неизменяемая система. Если будут заданы внешние силы, мы сможем при помощи уравнений статики найти как реакции опор, так и внутренние силовые факторы в любом поперечном сечении рамы. В той же раме, показанной на рис.5 б, кроме внешних наложены две дополнительные внутренние связи, запрещающие взаимное вертикальное и горизонтальное смещения точек А и В. Система в данном случае дважды статически неопределима (иногда добавляют: внутренним образом).

Рис. 6

В раме, показанной на рис. 4, а и б, также имеются внутренние дополнительные связи. Контур рамы полностью замкнут. Разрезая его в любом сечении (рис. 6), мы, не нарушая кинематической неизменяемости, получаем возможность при заданных силах найти внутренние силовые факторы в каждом сечении рамы. Следовательно, разрезая замкнутую раму, мы снимаем дополнительные связи, т.е. позволяем сечениям А и Б поворачиваться и смещаться в двух направлениях одно относительно другого. Обобщая, можно сказать, что замкнутый плоский контур имеет три дополнительные взаимные связи, т.е. трижды статически неопределим. Таким образом, рама, показанная на рис. 4 а, трижды статически неопределима, а рама, представленная на рис. 4, б, пять раз статически неопределима (три раза внутренним образом и два раза - внешним).

Рассмотрим теперь несколько примеров определения степени статической неопределимости стержневых и рамных систем. На рис. 7 показано несколько рам. Последовательно рассмотрим их.

а. Рама имеет четыре дополнительные внешние связи и три внутренние связи, т.е. семь раз статически неопределима.

б. Полагаем сначала, что шарнир А отсутствует. Тогда имеются две внешние и три внутренние дополнительные связи. Система без шарнира А была бы пять раз статически неопределимой.

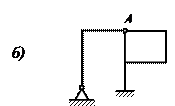
Рис 7

Шарнир А принадлежит одновременно трем стержням. Его можно рассматривать как два совпавших шарнира (рис.8). Так как каждый шарнир снимает одну связь, т.е. разрешает поворот одного сечения относительно другого, то можно сказать, что шарнир А снимает две связи. Система становится, таким образом, вместо пяти – три раза статически неопределимой.

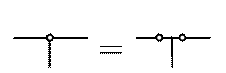
Рис 8

Обобщая сказанное, можно сделать вывод, что шарнир снимает число связей, на единицу меньшее числа сходящихся в нем стержней. В данном случае в шарнире А сходятся три стержня, и шарнир снимает две связи.

в. Если бы шарнир А отсутствовал, система была бы статически неопределимой четыре раза внешним образом и три раза внутренним образом, т.е. всего семь раз. Шарнир А снимает число связей, на единицу меньшее числа сходящихся в нем стержней, т.е. три связи. Рама четыре раза статически неопределима.

г. Рама три раза статически неопределима.

д. Внешние связи не удовлетворяют условиям кинематической неизменяемости. Это - механизм, точнее говоря, мгновенный механизм. Система имеет возможность поворачиваться относительно верхней опоры как жесткое целое. Понятно, что угол поворота будет небольшим. Нижняя связь заклинится и будет достигнуто какое-то положение равновесия:, но новое положение связей будет зависеть от жесткости системы. К раме неприменимы основные принципы сопротивления материалов: принцип неизменности начальных размеров и принцип независимости действия сил.

Дата добавления: 2014-01-07