
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Поверхностный интеграл второго рода
|
|
|
|
Задача о вычислении потока вектора через поверхность.
Пусть S – двусторонняя поверхность, то есть такая, что при движении точки по любому замкнутому пути, лежащему на поверхности, нормаль к поверхности возвращается в исходное состояние. (Примером односторонней поверхности является лист Мебиуса). Предположим, что через поверхность S протекает жидкость, причем скорость течения жидкости (ее направление и величина) различная в разных точках поверхности S. Таким образом, в точках поверхности задан вектор скорости
 ,
, 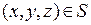 .
.
Будем считать функции  непрерывными на S.
непрерывными на S.
Потоком вектора 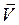 через поверхность S назовем объем жидкости, протекающей через поверхность S в направлении нормали к фиксированной стороне поверхности за единицу времени. Вычислим поток вектора через поверхность.
через поверхность S назовем объем жидкости, протекающей через поверхность S в направлении нормали к фиксированной стороне поверхности за единицу времени. Вычислим поток вектора через поверхность.
Будем считать поверхность гладкой, то есть имеющей касательную плоскость и нормаль в каждой точке. Разделим поверхность на n фрагментов 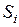 , настолько малых, что нормаль к этому поверхностному фрагменту в различных его точках практически совпадает с нормалью к
, настолько малых, что нормаль к этому поверхностному фрагменту в различных его точках практически совпадает с нормалью к 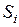 в одной выбранной на
в одной выбранной на 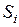 точке. Тогда поток
точке. Тогда поток 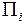 вектора
вектора 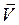 через фрагмент
через фрагмент 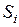 приблизительно равен
приблизительно равен 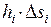 , где
, где 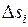 – площадь фрагмента,
– площадь фрагмента, 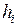 – проекция вектора
– проекция вектора 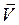 на направление нормали к выбранной стороне поверхностного фрагмента
на направление нормали к выбранной стороне поверхностного фрагмента 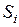 в точке
в точке 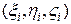 .
.

Следовательно, используя скалярное произведение, получим  , где
, где  – единичный вектор нормали к поверхностному фрагменту в точке
– единичный вектор нормали к поверхностному фрагменту в точке 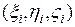 . Итак,
. Итак,  , причем значение
, причем значение 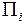 тем точнее, чем меньше площадь фрагмента
тем точнее, чем меньше площадь фрагмента 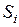 . Заметив, что площадь фрагмента
. Заметив, что площадь фрагмента 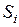 можно заменить площадью соответствующего фрагмента касательной в точке
можно заменить площадью соответствующего фрагмента касательной в точке 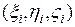 плоскости к S, получим:
плоскости к S, получим: 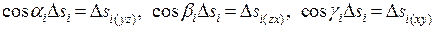 . Здесь
. Здесь  – площадь проекции фрагмента
– площадь проекции фрагмента 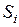 на плоскость YZ, взятая с тем знаком, какой имеет
на плоскость YZ, взятая с тем знаком, какой имеет  ,
,
 – площадь проекции фрагмента
– площадь проекции фрагмента 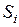 на плоскость ZX, взятая с тем знаком, какой имеет
на плоскость ZX, взятая с тем знаком, какой имеет  ,
,  – площадь проекции фрагмента
– площадь проекции фрагмента 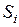 на плоскость XY, взятая с тем знаком, какой имеет
на плоскость XY, взятая с тем знаком, какой имеет 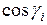 .
.
В итоге мы получим следующие выражения для вычисления потока:
 .
.
При переходе к пределу в последнем выражении, учитывая, что пределы элементов площадей на координатных плоскостях – это произведения дифференциалов соответствующих координат, получим
 .
.
Выражение в правой части последнего равенства называется поверхностным интегралом второго рода или поверхностным интегралом по координатам.
Заметим, что смена стороны поверхности меняет знак вектора нормали 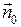 на противоположный, поэтому смена стороны поверхности меняет знак соответствующего интеграла второго рода на противоположный.
на противоположный, поэтому смена стороны поверхности меняет знак соответствующего интеграла второго рода на противоположный.
Следует отметить, что поверхностный интеграл второго рода иногда записывают в виде
 ,
,
где  – направляющие векторы нормали к поверхности.
– направляющие векторы нормали к поверхности.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 380; Нарушение авторских прав?; Мы поможем в написании вашей работы!