
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Способ вычисления поверхностного интеграла второго рода
|
|
|
|
Пусть требуется вычислить криволинейный интеграл  , когда функции
, когда функции 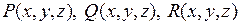 непрерывны на поверхности S. Поверхность S задана параметрически:
непрерывны на поверхности S. Поверхность S задана параметрически: 
 , где функции
, где функции  имеют непрерывные в прямоугольнике
имеют непрерывные в прямоугольнике 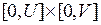 частные производные первого порядка, причем
частные производные первого порядка, причем 
 . Разобьем прямоугольник значений параметров
. Разобьем прямоугольник значений параметров 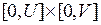 на прямоугольники
на прямоугольники 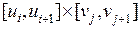 ,
, 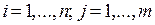 . Соответственно такому разбиению прямоугольника параметров мы получим разбиение поверхности S на фрагменты
. Соответственно такому разбиению прямоугольника параметров мы получим разбиение поверхности S на фрагменты 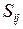 . Выберем
. Выберем  . Тогда на каждом фрагменте
. Тогда на каждом фрагменте 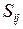 мы получим точку
мы получим точку 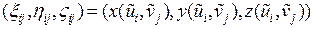 . Используем то, что
. Используем то, что 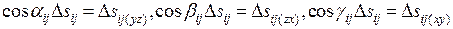 , где
, где 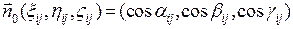 – единичный вектор нормали к поверхности в точке
– единичный вектор нормали к поверхности в точке 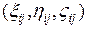 . Согласно известной формуле для получения вектора нормали к поверхности, заданной параметрически, получим:
. Согласно известной формуле для получения вектора нормали к поверхности, заданной параметрически, получим:  – вектор нормали к поверхности S в точке
– вектор нормали к поверхности S в точке 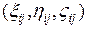 , где знаки + или – выбираются в зависимости от выбора стороны поверхности. Для того, чтобы получить единичный вектор
, где знаки + или – выбираются в зависимости от выбора стороны поверхности. Для того, чтобы получить единичный вектор  , следует поделить вектор
, следует поделить вектор  на его длину, равную
на его длину, равную  . Теперь, учитывая, что
. Теперь, учитывая, что  ,
,
где  , имеем
, имеем

Переходя к пределу, получим формулу сведения поверхностного интеграла второго рода к двойному интегралу по области значений параметров:
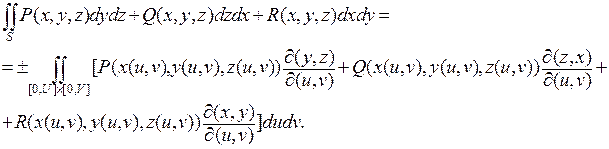
Выбор знаков + или – определяется выбором стороны поверхности.
П р и м е р ы.
1. Вычислить  , где S – внешняя сторона эллипсоида
, где S – внешняя сторона эллипсоида  .
.
Р е ш е н и е. Параметризуем уравнение эллипсоида с помощью обобщенных сферических координат: 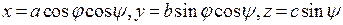 ,
, 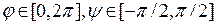 . Вычислим соответствующие якобианы:
. Вычислим соответствующие якобианы:
 . Чтобы определить, какой знак нужно будет выбрать, обратим внимание на то, что внешняя нормаль к эллипсоиду в тех точках, где
. Чтобы определить, какой знак нужно будет выбрать, обратим внимание на то, что внешняя нормаль к эллипсоиду в тех точках, где  , то есть,
, то есть,  , имеет положительную проекцию на ось OZ. Это означает, что третья координата вектора нормали при
, имеет положительную проекцию на ось OZ. Это означает, что третья координата вектора нормали при  должна быть положительной. В нашем случае
должна быть положительной. В нашем случае  при
при  , следовательно, найденные якобианы являются координатами вектора нормали именно к внешней стороне эллипсоида, и менять знак у интеграла не придется. Таким образом,
, следовательно, найденные якобианы являются координатами вектора нормали именно к внешней стороне эллипсоида, и менять знак у интеграла не придется. Таким образом,
 .
.
2. Найти поток вектора  через сферу
через сферу 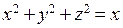 .
.
Р е ш е н и е. Параметризуем поверхность: 
Так как  , нам для вычисления потока через параметризованную поверхность необходимо подсчитать якобианы, чтобы перейти в интеграле к переменным
, нам для вычисления потока через параметризованную поверхность необходимо подсчитать якобианы, чтобы перейти в интеграле к переменным  и
и 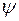 . Имеем
. Имеем  . Поэтому вычисление потока сводится к вычислению интеграла
. Поэтому вычисление потока сводится к вычислению интеграла  с применением MAXIMы.
с применением MAXIMы.
3. Вычислить поток вектора  через боковую поверхность цилиндра
через боковую поверхность цилиндра  .
.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 652; Нарушение авторских прав?; Мы поможем в написании вашей работы!