Структурные методы расчета Н

– это методы прямого вычисления Н, объектов по известной Н, их элементов.

Необходимое условие их применения – независимость отказов элементов. Они являются основными методами расчета показателей БО, РП и КПН объектов, поддающихся разукрупнению на элементы, Н которых на момент расчета уже известна.

Их применяют также для расчета показателей Д и 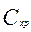объектов, критерии 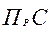которых выражаются через Д и 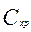их элементов.

Таким образом, структурные методы дают приемлемые результаты при расчете Н. электрических, электронных, р/эл-х объектов, а также ряда механических систем, разукрупненных до уровня конструктивно-функциональных единиц (узлы гидросистем, коробка передач, бортовой редуктор, двигатель и т.п.), отказы которых являются независимыми.

Расчет Н структурными методами включает:

- представление О в виде структурной схемы, т.е. в виде совокупности определенным образом соединенных в смысле Н элементов (составление ССН);

- описание ССН адекватной математической моделью, позволяющей в рамках принятых допущений вычислить ПН О по данным о Н его элементов.

3.1.а) Расчет показателей безотказности при постоянном резервировании

При постоянном резервировании все элементы находятся под нагрузкой и поэтому нельзя выделить в объекте основные и резервные элементы. Все они «равноправны».

Методику расчета ПБ при постоянном резервировании будем рассматривать на примере восстанавливаемых объектов.

Известны:

-конструкция объекта (его элементный состав и структура);

-интенсивность отказов элементов – 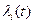, i=1,…,n.

Определить:

-ВБР объекта в течение заданной наработки t – P(t);

-среднюю наработку до 1-го отказа – Т₁;

-параметр потока отказов объекта – Ω(t).

Допущение:

-поток отказов элементов – простейший.

Уяснение задачи:

1.Вид объекта – восстанавливаемый

2.Так как ПБО рассчитываются до 1-го отказа(например с целью установления гарантийной наработки), то очевидно, что

Т₁=Тс для НВО

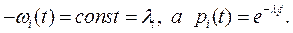3.Так как поток отказов элементов простейший, то:

- отказы элементов – события независимые;

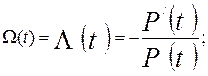4.В данной задаче достаточно определить Р(t) в виде функции, т.к. остальные показатели можно вычислить через P(t) по следующим зависимостям:

.

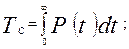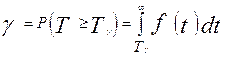В дальнейшем покажем только методику определения вероятности безотказной работы.

Задача I. Рассмотрим объект, состоящий из «n» последовательно соединенных (в смысле надежности) элементов, вероятность безотказной работы которых равна .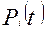

В каком случае эта «цепочка» будет работать?

В том случае, если все элементы работоспособны. Формализуем этот ответ. С этой целью введём: событие А – заключающееся в безотказной работе объекта;

событие А_i – заключающееся в безотказной работе i – го элемента.

Тогда А будет иметь место при совместном выполнении всех событий А_i, что соответствует их произведению, то есть

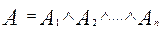
Так как события А и А_i случайны, определим их вероятности

,

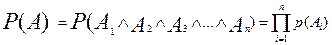что в терминах решаемой задачи равносильно

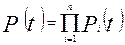- математическая модель ССН объекта.

Правило 1. При расчете ВБР, цепь последовательно соединенных (в смысле надежности) элементов можно заменить одним элементом с вероятностью безотказной работы равной произведению вероятностей безотказной работы всех элементов этой цепи.

Задача II. Рассмотрим объект, состоящий из «m» параллельно соединенных (в смысле надежности) элементов, вероятность безотказной работы которых равна 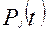, j=1,…,m.

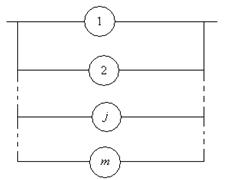
Вопрос: В каком случае откажет эта подсистема?

В том случае, если откажут все элементы. Формализуем этот ответ. С этой целью введём: событие B – заключающееся в отказе подсистемы;

событие Bj – заключающееся в отказе j – го элемента.

Тогда B будет иметь место при совместном выполнении всех событий Bj, что соответствует их произведению, то есть

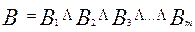
Так как события B и Bj случайны, определим их вероятности

,

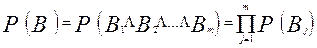что в терминах решаемой задачи равносильно

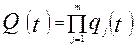
Правило 2. При расчете ВО подсистемы, состоящей из параллельно соединенных (в смысле надежности) элементов, их можно заменить одним, с вероятностью отказа равной произведению вероятностей отказа всех элементов этой подсистемы.

Это выражение легко преобразовать, если учесть, что

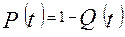
Окончательно получим:

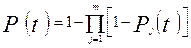- математическая модель ССН подсистемы.

Если все элементы звена равнонадёжны, то последняя зависимость при ЭЗР примет вид

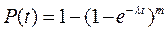
Вычислим среднюю наработку до отказа подсистемы.

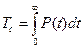Известно, что Определим P(t).

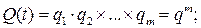Используя правило (П 2), получим:

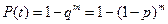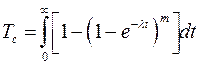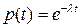При ЭЗР имеем: Тогда

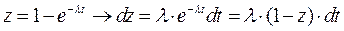Введем переменную

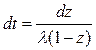Отсюда

Определим пределы z. При t=0→z=0; t = ∞ → z=1.

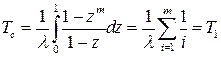Поэтому

Пользуясь этими правилами, легко рассчитать ВБР любого объекта при постоянном смешанном резервировании.

Рассчитаем ВБР системы, ССН которой приведена на рисунке при известной ВБР её элементов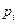

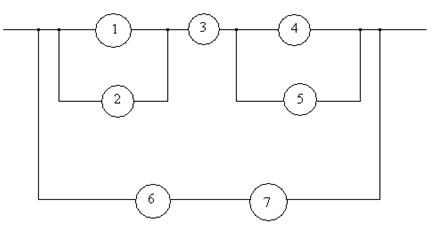
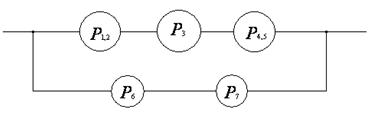
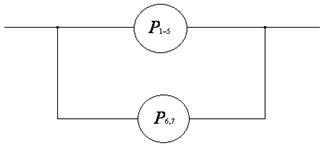
I)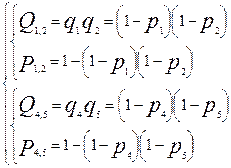

II)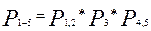

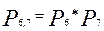
III) ;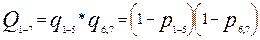

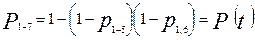
Рассмотренная методика определения ПБО при постоянном резервировании справедлива в том случае, если при отказе какого-либо элемента условия работы других не изменяется.

3.1. б) Расчет показателей безотказности при резервировании замещением

Резервирование замещением – это резервирование, при котором функции основного элемента передаются резервному только после отказа основного элемента. при этом резервные элементы до включения, как правило, могут находиться в облегченном или ненарушенном режиме (например, запасные части).

Расчет показателей безотказности при резервировании замещением рассмотрим на следующем примере.

Дано: -объект, состоящий из одного основного и «m» резервных элементов, рис.1,3

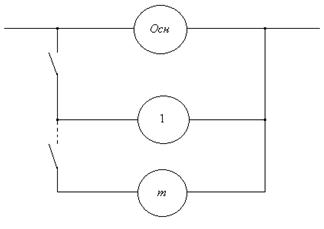
Рис.1.3.

-интенсивность отказов элементов ;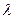

-так как 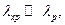то модель функционирования такого объекта можно представить в виде: при отказе основного элемента включается первый резервный, после отказа первого – второй резервный и т.д.

Определить показатели БО:

; ;

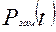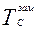Допущения:

1. Поток отказов элементов простейший.

2. Переключатели абсолютно надежны.

Вопрос: Когда объект будет работоспособным?

Условием нормального функционирования объекта является работоспособность хотя бы одного элемента. Реализация этого условия возможна при разных состояниях объекта.

Проведем рассуждения о возможных ситуациях РБТС объекта.

Пусть Н – событие, заключающееся в безотказной работе объекта. Оно будет иметь место при следующих событиях:

- при 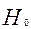- событие, заключающееся в безотказной работе основного элемента;

- или при 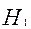- событии, заключающемся в отказе одного (основного) элемента;

- или при 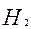- событии, заключающемся в отказе двух элементов (основного и первого резервного элемента);

- или при ………………………

- или при 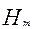- событии, заключающемся в отказе m элементов (основного и первого, второго,…,(m-1) резервных элементов).

Тогда событие Н будет иметь место при возникновении хотя бы одного события 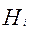, что по определению соответствует сумме m событий, т.е. 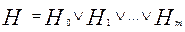, т.к. по определению «Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий».

Так как рассматриваемые события случайны, определим их вероятности

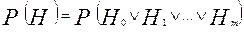
События 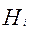являются несовместными. В соответствии с теоремой сложения вероятностей – вероятность суммы несовместных событий равна сумме вероятностей этих событий.

,

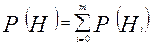где: 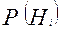- вероятность того, что откажут ровно i элементов.

Известно, что в условиях простейшего потока отказов случайное число отказов для резервирования замещением подчиняется распределению Пуассона, в соответствии с которым вероятность появления ровно i событий (в данном случае отказов) равна:

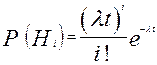, тогда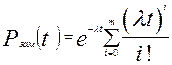

К данной схеме может быть приведен любой объект, состоящий из n последовательно (в смысле надежности) соединённых элементов и имеющий m таких же резервных цепей (рис. 1.4). В самом деле, n последовательных элементов можно заменить одним с интенсивностью отказов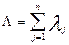

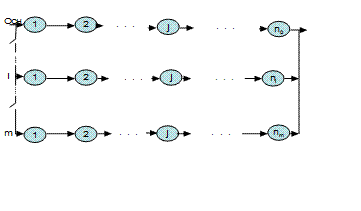
Рис. 1.4.

Тогда ВБР этого объекта вычисляется по зависимости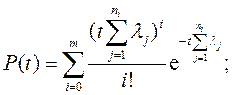

Если все элементы в каждой цепи будут равнонадёжны, то его ВБР можно вычислить по зависимости

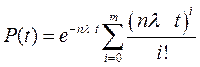
Средняя наработка до отказа определяется по зависимости:

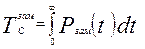
Подставив сюда выражение 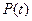и проинтегрировав, получим:

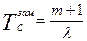
или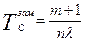

Этот же результат можно получить из простых рассуждений, представив себе функционирование объекта. Основной элемент будет иметь среднюю наработку равную 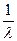, первый резервный - 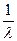и т.д. Поскольку число элементов (m+1), то средняя наработка объекта равна сумме средних наработок (m+1) элементов, что и выражают последние две формулы.

Дата добавления: 2014-01-07