Сущность МНК

Рассмотрим на более простом примере, когда y является функцией только одного фактора x. Тогда исходные данные, собранные по объектам-аналогам, будут иметь вид

X	X1	X2	...	Xj	...	Xm
Y	Y1	Y2	...	Yj	...	Ym

Задача же как мы помним заключается в получении модели вида (1), в данном случае в виде двучлена

.

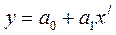Проведём графическую аппроксимацию данных таблицы. Для этого нанесём точки Xj и Yj на плоскость координат XOY. В данном случае теоретический закон имеет вид прямой линии, уравнение которо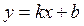й или .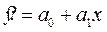

Следует заметить, что не все опытные точки совпадают с графиком, а имеют некоторые отклонения от него . Очевидно, что эта линия должна располагаться на плоскости координат так, чтобы отклонения, точнее сумма отклонений опытных точек от неё были минимальными. Чем определяется положение этой линии на плоскости? Значениями коэффициентов и их знаками. Следовательно, задача состоит в отыскании именно таких коэффициентов. Как её решить?

x

Выразим сказанное математически и найдём этот минимум.

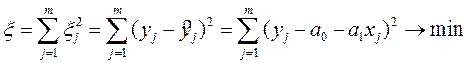
Как это сделать? Самый простой приём, известный в математике это взятие первой производной от функции, приравнивание её к нулю и нахождение такого значения аргумента X, при котором функция обращается в минимум.

Тогда

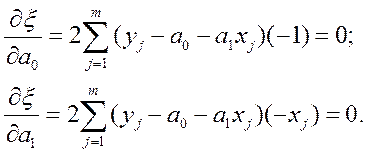
После несложных преобразований, получим

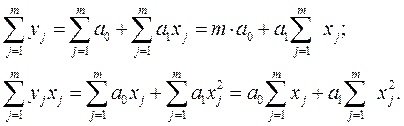
Решив эту систему уравнений, получим значения искомых коэффициентов 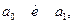найденных при условии обеспечения минимума ошибки адекватности принятой модели. Т. о. задача решена.

В общем случае решение задачи приводится ниже:

1). Имеются данные о значениях y_j и x_rj, j=1,...,m, собранные наблюдением за объектами-аналогами.

2). Эти данные аппроксимируются моделью вида (1) так, чтобы сумма квадратов отклонений опытных точек от поверхности (линии), заданной моделью, была минимальной, то есть:

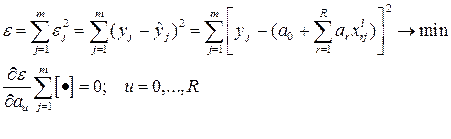
Отсюда система нормальных уравнений R+1 с R+1 неизвестными a₀,…a_R.

В качестве примера такой модели можно привести уравнение связи, полученное профессором Есиным для машин гусеничного типа, устанавливающее естественную связь между средним временем их восстановления Т_В и КТФ.

X₁ – масса проектируемого образца, т.

X₂ - удельная мощность, кВт/кг.

X₃ – число выполняемых машиной функций.

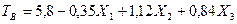
Зная значения X₁, X₂, X₃ (они должны быть известны в техническом задании), подставим их в модель и получаем прогнозную оценку Т_В для перспективного образца, которая после критического анализа закладывается в техническое задание.

3.3 Физические (параметрические) методы расчета надежности.

Применяют для расчета БО, Д и Схр О, для которых известны их механизмы деградации под влиянием внешних и внутренних факторов.

Методы основаны на описании процессов деградации математическими моделями непревышения или накопления повреждений, позволяющими вычислить ПН по свойствам материалов, используемых в объекте с учетом его конструкции, планируемой технологии изготовления и условий эксплуатации.

Здесь имеется ввиду непревышение нагрузок над «несущей способностью». Поскольку и те и другие в общем случае являются случайными величинами, то решение задач в рамках этих моделей базируются на вероятностных подходах.

По схеме моделей непревышения или мгновенного разрушения состояние конструкции изменяется не монотонно, то приближаясь, то удаляясь и опять приближаясь к Пр и так до тех пор, пока не достигнет его. Прс в рамках этой схемы наступает при условии S>R,

Здесь S-нагрузка;

R-несущая способность конструкции

Очевидно, что область безотказной работы определяется условием не превышения S<R.

Пусть S и R случайные величины имеющие нормальное распределение с параметрами

m_s, 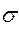_s

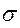m_R,_R

В качестве параметра состояния конструкции (элемента) примем разность

Х=R-S

Найдем вероятность не разрушения элемента, то есть P(x>0)

Т. к. случайный параметр Х является композицией нормального распределения СВ S и R, то он также подчиняется НЗР с параметрами

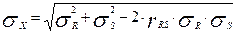
где 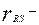коэффициент корреляции СВ R и S.

Плотность нормального распределения параметра Х имеет вид

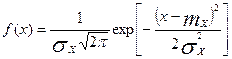
Т.к. X=R=S, то очевидно что элемент будет работать безотказно при Х>0.Вероятность этого события равна площади под кривой f(х) при Х>0

x

Аналитически она вычисляется по зависимости

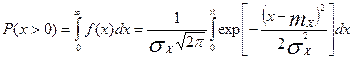, (1)

при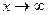

Введем переменную , тогда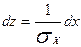

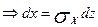
Определим пределы изменения новой переменной z

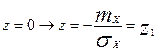, при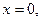

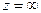
Подставив полученное в (1) будем иметь

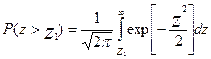
Геометрическая трактовка последнего

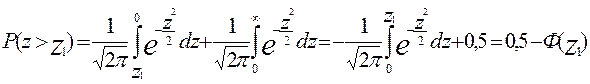
где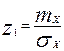

Т.е.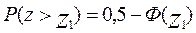

Следует учесть, что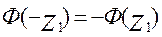

На практике удобнее оперировать не абсолютными величинам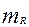и 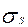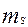и , и 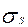, а величинами относительными:

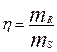-- средне статистический коэффициент запаса несущей способности.

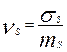-и - коэффициенты вариации нагрузки и несущей способности.

В этих условиях 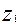будет определяться зависимостью

,

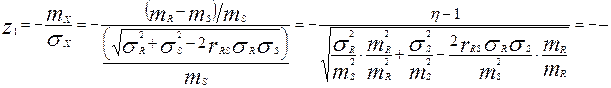
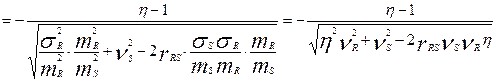Т.к. в большинстве случаев S и R статистически независимы, то 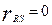. Тогда 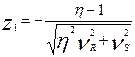, (2)

Т.е. ВБР элемента ,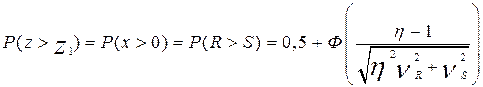

Используя (2) можно решить и обратную задачу – задавшись требуемой ВБР. 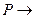определить 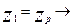а из (2) определить запас прочности 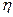, обеспечивающий требуемую ВБР.

Последняя зависимость позволяет вычислить коэффициент запаса несущей способности т.е. характеристику нагруженного резерва при заданной ВБР конструкции .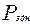

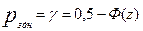,откуда 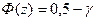.Т.к. 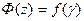, то и

.

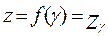В этих условиях коэффициент запаса несущей способности 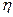вычисляется по зависимости

,

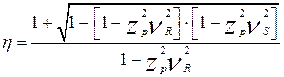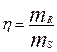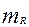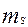Этот результат получен для ,для случая когда ине зависят от времени.

Подход Проникова

В н/вр используются 2 класса моделей непревышения:

-многопараметрические

-однопараметрические

S ₃

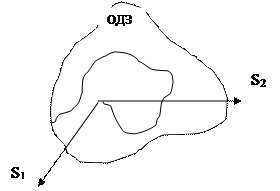
Рис.1

Многопараметрическая модель может быть представлена моделью выбросов некоторого случайного процесса за границы допустимой области.

Например:

-состояние объекта характеризуется параметрами S₁, S₂, S₃;

-известны их допустимые значения;

-границы детерминированы.

Геометрическая трактовка модели выглядит следующим образом (см. рис.1).

В этом случае ПН- ВБР объекта будет иметь

P(t)=P(S)

Следует иметь в виду, что параметров, определяющих ТС объекта много, они, как правило, имеют различную физическую природу, характеризуются различными распределениями, поэтому модели очень сложны и допускают прямые аналитические решения лишь в редких случаях.

Основным методом их решения является статистическое моделирование.

Профессором Прониковым предложены модели, разрешаемые последовательно для ряда независимых параметров S_к, к=1,...,К с последующим обобщением полученных результатов.

Сущность определения значений ПН в рамках данной модели в следующем.

1. На основе анализа функциональной схемы объекта выбирается статистически независимые выходные параметры 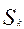, k=1, .

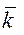2. Определяется вероятность безотказной работы О по каждому из параметров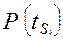, k=1, .

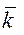Например, в условиях нормального распределения значения параметра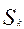

где: Ф – функция Лапласа, значение которой табулировано;

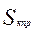- предельное значение выходного параметра;

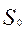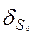, - МОЖ и СКО выходные параметры при t = 0;

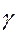- скорость деградации параметра;

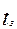- заданный временной интервал;

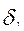- СКО скорости деградации параметра.

3. Определяется ВБР объекта по всем выходным параметрам.

.

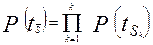Хотя решение однопараметрических моделей проще многопараметрических, тем не менее и здесь возникает достаточно много трудностей, основными из которых являются получение на стадии проектирования достоверных оценок таких величин, как 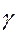и .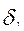

Дата добавления: 2014-01-07