
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Построение нечетких правил
|
|
|
|
Проектирование базы нечетких правил на основе численных данных
При решении большинства прикладных задач регулирования информацию, необходимую для построения и реализации системы управления, можно разделить на две части: численную (количественную), получаемую с измерительных датчиков, и лингвистическую (качественную), поступающую от эксперта. Значительная часть нечетких систем регулирования использует второй вид знаний, чаще всего представляемых в форме базы нечетких правил.
В случае, когда возникает необходимость спроектировать нечеткую систему, но в наличии имеются только численные данные, мы сталкиваемся с серьезными проблемами. Одним из путей их разрешения считаются так называемые нейро-нечеткие (fuzzy-neural) системы, представленные в главе 5. Они обладают многими достоинствами, однако сдерживающим моментом является длительность наполнения их знаниями (построения базы правил) в процессе итеративного обучения. Далее излагается один из простейших, но в то же время весьма универсальный метод построения базы нечетких правил на основе численных данных [30, 31]. Достоинства этого метода заключаются в его необычайной простоте и очень высокой эффективности. Кроме того, он позволяет объединять численную информацию, представленную в форме обучающих данных, с лингвистической информацией, имеющей вид базы правил, за счет дополнения имеющейся базы правилами, созданными на основе численных данных.
Допустим для упрощения, что мы создаем базу правил для нечеткой системы с двумя входами и одним выходом. Очевидно, что для этого необходимы обучающие данные в виде множества пар
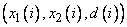 ,
,  (3.278)
(3.278)
где 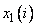 ,
, 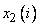 - сигналы, подаваемые на вход модуля нечеткого управления, а
- сигналы, подаваемые на вход модуля нечеткого управления, а 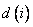 - ожидаемое (эталонное) значение выходного сигнала. Задача заключается в формировании таких нечетких правил, чтобы сконструированный на их основе модуль управления при получении входных сигналов генерировал корректные (имеющие наименьшую погрешность) выходные сигналы.
- ожидаемое (эталонное) значение выходного сигнала. Задача заключается в формировании таких нечетких правил, чтобы сконструированный на их основе модуль управления при получении входных сигналов генерировал корректные (имеющие наименьшую погрешность) выходные сигналы.
Шаг 1. Разделение пространств входных и выходных сигналов на области.
Представим, что нам известно минимальное и максимальное значения каждого сигнала. По ним можно определить интервалы, в которых находятся допустимые значения. Например, для входного сигнала  такой интервал обозначим
такой интервал обозначим  . Если значения
. Если значения 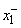 и
и  неизвестны, то можно воспользоваться обучающими данными и выбрать из них соответственно минимальное и максимальное значения
неизвестны, то можно воспользоваться обучающими данными и выбрать из них соответственно минимальное и максимальное значения
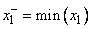 ,
, 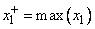 .
.
Аналогично для сигнала  определим интервал
определим интервал 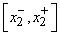 , а для эталонного сигнала
, а для эталонного сигнала 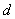 - интервал
- интервал 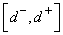 .
.
Каждый определенный таким образом интервал разделим на 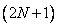 областей (отрезков), причем значение
областей (отрезков), причем значение 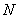 для каждого сигнала подбирается индивидуально, а отрезки могут иметь одинаковую или различную длину. Отдельные области обозначим следующим образом:
для каждого сигнала подбирается индивидуально, а отрезки могут иметь одинаковую или различную длину. Отдельные области обозначим следующим образом: 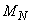 (Малый
(Малый 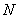 ),...,
),..., 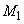 (Малый 1),
(Малый 1), 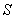 (Средний),
(Средний), 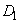 (Большой 1),...,
(Большой 1),..., 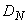 (Большой
(Большой 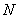 ) и для каждого из них определим одну функцию принадлежности. На рис. 3.37 представлен пример такого разделения, где область определения сигнала
) и для каждого из них определим одну функцию принадлежности. На рис. 3.37 представлен пример такого разделения, где область определения сигнала  разбита на пять подобластей
разбита на пять подобластей  , сигнала
, сигнала  - на семь подобластей
- на семь подобластей  , тогда как область определения выходного сигнала
, тогда как область определения выходного сигнала 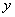 - на пять подобластей
- на пять подобластей  .
.
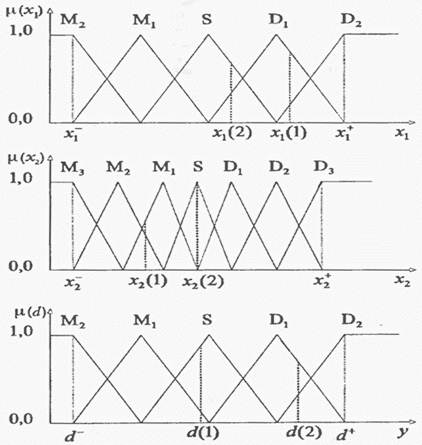
Рис. 1 – Разделение пространств входных и выходных сигналов на области и соответствующие им функции принадлежности.
Каждая функция принадлежности имеет треугольную форму; одна из вершин располагается в центре области и ей соответствует значение функции, равное 1. Две других вершины лежат в центрах соседних областей, им соответствуют значения функции, равные 0. Очевидно, что такое разделение выбрано для примера. Можно предложить много других способов разделения входного и выходного пространства на отдельные области и использовать другие формы функций принадлежности.
Шаг 2. Построение нечетких правил на основе обучающих данных.
Вначале определим степени принадлежности обучающих данных (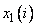 ,
, 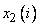 и
и 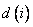 ) к каждой области, выделенной на шаге 1. Эти степени будут выражаться значениями функций принадлежности соответствующих нечетких множеств для каждой группы данных. Например, для случая, показанного на рис. 1, степень принадлежности данного
) к каждой области, выделенной на шаге 1. Эти степени будут выражаться значениями функций принадлежности соответствующих нечетких множеств для каждой группы данных. Например, для случая, показанного на рис. 1, степень принадлежности данного 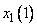 к области
к области 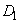 составляет 0,8, к области
составляет 0,8, к области 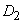 - 0,2, а к остальным областям - 0. Аналогично для данного
- 0,2, а к остальным областям - 0. Аналогично для данного 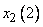 степень принадлежности к области
степень принадлежности к области 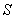 составляет 1, а к остальным областям - 0. Теперь сопоставим обучающие данные
составляет 1, а к остальным областям - 0. Теперь сопоставим обучающие данные 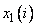 ,
, 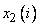 и
и 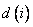 областям, в которых они имеют максимальные степени принадлежности. Заметим, что
областям, в которых они имеют максимальные степени принадлежности. Заметим, что 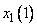 имеет наибольшую степень принадлежности к области
имеет наибольшую степень принадлежности к области 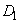 , а
, а 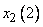 - к области
- к области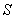 . Окончательно для каждой пары обучающих данных можно записать одно правило, т.е.
. Окончательно для каждой пары обучающих данных можно записать одно правило, т.е.


 : IF (
: IF ( это
это 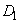 AND
AND  это
это 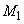 ) THEN
) THEN 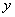 это
это 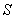 ;
; 


 : IF (
: IF ( это
это 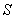 AND
AND  это
это 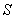 ) THEN
) THEN 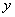 это
это 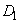 .
.
Шаг 3. Приписывание каждому правилу степени истинности.
Как правило, в наличии имеется большое количество пар обучающих данных, по каждой из них может быть сформулировано одно правило, поэтому существует высокая вероятность того, что некоторые из этих правил окажутся противоречивыми. Это относится к правилам с одной и той же посылкой (условием), но с разными следствиями (выводами). Один из методов решения этой проблемы заключается в приписывании каждому правилу так называемой степени истинности с последующим выбором из противоречащих друг другу правил того, у которого эта степень окажется наибольшей. Таким образом, не только разрешается проблема противоречивых правил, но и значительно уменьшается их общее количество. Для правила вида
 : IF (
: IF ( это
это  AND
AND  это
это  ) THEN (
) THEN (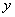 это
это  )
)
степень истинности, обозначаемая как  , определяется как
, определяется как
 .
.
Таким образом, первое правило  из нашего примера имеет степень истинности
из нашего примера имеет степень истинности
 (3.282)
(3.282)
а второе правило -
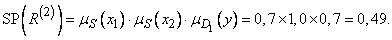 (3.283)
(3.283)
Шаг 4. Создание базы нечетких правил.
Способ построения базы нечетких правил представлен на рис. 2. Эта база представляется таблицей, которая заполняется нечеткими правилами следующим образом: если правило имеет вид
 : IF (
: IF ( это
это 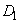 AND
AND  это
это 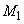 ) THEN
) THEN 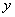 это
это 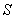 , (3.284)
, (3.284)
то на пересечении строки 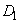 (соответствующей сигналу
(соответствующей сигналу  ) и столбца
) и столбца 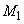 (сигнал
(сигнал  ) вписываем название нечеткого множества, присутствующего в следствии, т.е.
) вписываем название нечеткого множества, присутствующего в следствии, т.е. 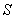 (соответствующего выходному сигналу
(соответствующего выходному сигналу 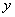 ). Если имеется несколько нечетких правил с одной и той же посылкой, то из них выбирается то, которое имеет наивысшую степень истинности.
). Если имеется несколько нечетких правил с одной и той же посылкой, то из них выбирается то, которое имеет наивысшую степень истинности.
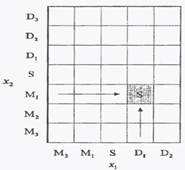
Рис. 2 – Форма базы нечетких правил
Шаг 5. Дефуззификация.
Наша задача заключается в определении с помощью базы правил отображения 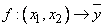 , где
, где 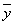 - выходная величина нечеткой системы. При определении количественного значения управляющего воздействия
- выходная величина нечеткой системы. При определении количественного значения управляющего воздействия 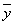 для данных, входных сигналов
для данных, входных сигналов 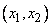 необходимо выполнять операцию дефуззификации. Вначале для входных сигналов
необходимо выполнять операцию дефуззификации. Вначале для входных сигналов 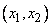 с использованием операции произведения объединим посылки (условия)
с использованием операции произведения объединим посылки (условия)  –го нечеткого правила. Таким образом, определяется так называемая степень активности
–го нечеткого правила. Таким образом, определяется так называемая степень активности  –го правила. Ее значение рассчитывается по формуле
–го правила. Ее значение рассчитывается по формуле
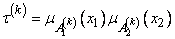 . (3.285)
. (3.285)
Например, для первого правила  степень активности определяется выражением
степень активности определяется выражением
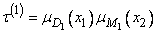 . (3.286)
. (3.286)
Для расчета выходного значения 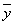 воспользуемся способом дефуззификации по среднему центру (3.269)
воспользуемся способом дефуззификации по среднему центру (3.269)
 . (3.287)
. (3.287)
Рассмотренный метод легко можно обобщить на случай нечеткой системы с любым числом входов и выходов. На рис. 3 представлен алгоритм построения базы правил в виде блок-схемы, которая может служить основой для подготовки соответствующей программной реализации.
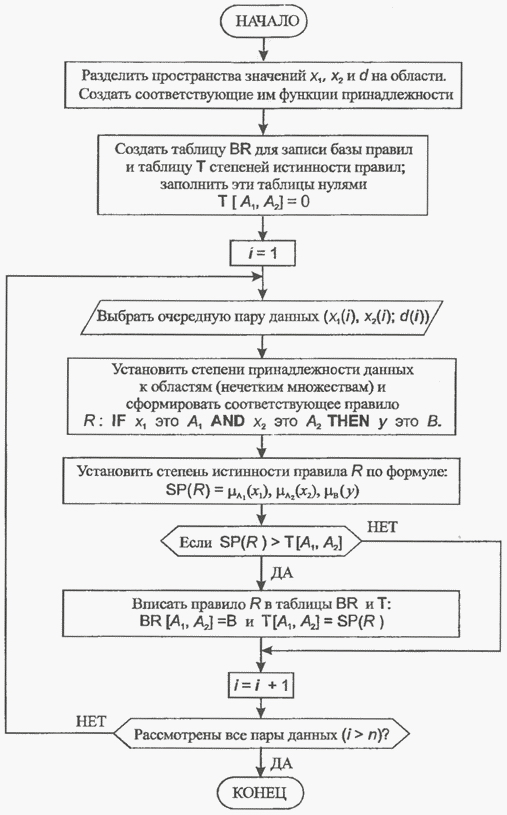
Рис. 3 – Блок-схема построения базы правил на основе численных данных.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1848; Нарушение авторских прав?; Мы поможем в написании вашей работы!