Виды структурных (непараметрических) средних

Вид Средней	Методика расчета показателя
Мода	В интервальных рядах с равными интервалами мода вычисляется по формуле 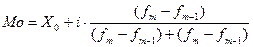, Где X0 – минимальная граница модального интервала; i – величина модального интервала; fm – частота модального интервала; fm-1 – частота интервала, предшествующего модальному интервалу; fm+1 – частота интервала, следующего за модальным.   Модальный интервал в интервальном ряду определяется по наибольшей частоте
Медиана	В дискретном вариационном ряду определение медианного значения признака сводится к определению номера медианной единицы ряда по формуле , где n – объем совокупности. Полученное значение показывает, где точно находится номер медианной единицы (номер середины ряда). Медианное значение характеризуется тем, что его кумулятивная частота (сумма накопленных частот по группам) равна половине суммы всех частот или превышает ее. В интервальном ряду с равными интервалами медиана рассчитывается по формуле , где X0 – начальное значение медианного интервала; i - величина медианного интервала; ∑ f – сумма частот ряда; Sm-1 - сумма накопленных частот в интервалах, предшествующих медианному; fm – частота медианного интервала.   Для определения медианного интервала необходимо рассчитать суммы накопленных частот. Медианный интервал характерен тем, что его кумулятивная частота равна полусумме всех частот ряда или превышает ее
Квартили	Значения признака, делящие ранжированную совокупность на четыре равные части. Различают нижний квартиль (Q1), отделяющий ¼ часть совокупности с наименьшими значениями признака, и верхний квартиль (Q3), отсекающий ¼ часть с наибольшими значениями признака. Средний квартиль (Q2) совпадает с медианой (Me). Для расчета квартилей по интервальному вариационному ряду используют формулы ; , где XQ1 (XQ3) – нижняя граница интервала, содержащего нижний квартиль (верхний) квартиль; i - величина интервала; SQ1-1 (SQ3-1) – накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль (верхний) квартиль; f Q1 (f Q3) – частота интервала, содержащего нижний квартиль (верхний) квартиль
Децили	Варианты, делящие ранжированный ряд на десять равных частей; они вычисляются по той же схеме, что и квартили: ; и т.д.
Квинтили	Значения признака, делящие ряд на пять равных частей. Они вычисляются по той же схеме, что квартили и децили
Перцентили	Значения признака, делящие ряд на 100 равных частей

Дата добавления: 2014-01-07