Входящий поток заявок

Определение 1. Потоком требований (входящим потоком) называется совокупность заявок на обслуживание, поступающих в обслуживающую систему.

Изучение потока требований является первой задачей, которая возникает при исследовании работы системы массового обслуживания.

Поток требований может быть описан некоторой случайной функцией Х(t), определяющей число требований, передающихся в обслуживании за промежуток времени (0,t]. Х(t) – случайный процесс с непрерывным временем и дискретным множеством значений, причем Х(t) может принимать только целые значения и с возрастанием t не убывает.

График реализации процесса имеет вид, изображенный на рис.2.

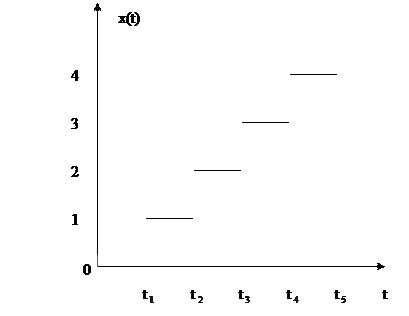
Рис.2.

Для задания случайного процесса Х(t) достаточно знать вероятности 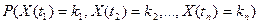для любых 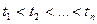и любых 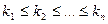. Но задача отыскания таких вероятностей в общем случае является весьма трудной.

Часто на практике встречаются потоки, обладающие свойствами, позволяющими найти более простые способы их описания. Так многие потоки требований обладают свойством стационарности.

Определение 2. Входящий поток называется стационарным, если для любого натурального n, любых моментов времени 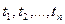таких, что 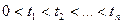, и любого а>0 совместное распределение случайных величин 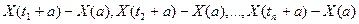не зависит от а.

В частности, 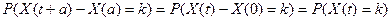для n=1,2,… и всех 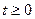. (Последнее равенство следует из условия Х(0)=0.)

Свойство стационарности означает, что вероятность поступления определенного числа требований в интервале (а, а+t) не зависит от начала отсчета времени а, а зависит от длины интервала t.

Свойством стационарности обладают многие реальные потоки, например, поток вызовов, поступающих на АТС. Правда, в течение суток режим работы АТС может меняться в значительных пределах, поэтому поток вызовов следует считать стационарным лишь на отдельных отрезках времени.

Определение. Поток требований называется потоком без последействия, если для любых моментов времени 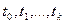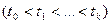случайные величины 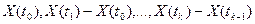будут взаимно независимы.

Свойство отсутствия последействия означает, что число требований, поступивших в систему за промежуток времени 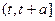, не зависит от того, сколько требований поступило в систему до момента времени t.

Обозначим 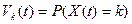, где 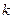=0,1,2,…

Теорема 1. Стационарный поток без последействия полностью характеризуется системой функций 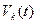, 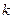=0,1,2,…

Доказательство. Пусть 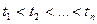, 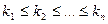. Рассмотрим 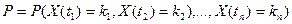. Положим 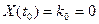, тогда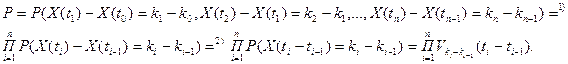

Переход 1) следует из свойства отсутствие последействия, а переход 2) из условия стационарности.

Обозначим через 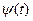вероятность появления за промежуток времени (0, t] по крайней мере двух требований.

Определение 4. Стационарный поток требований называется ординарным, если .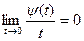

Ординарность потока требований выражает собой условие практической невозможности появления двух или более требований в один и тот же момент времени.

Особый интерес представляют так называемые простейшие потоки. Потоки такого типа или близкие к ним часто встречаются на практике.

Определение 5. Простейшим потоком требований называется поток, обладающий одновременно свойствами стационарности, ординарности и отсутствия последствия.

Так как простейший поток является стационарным и у него отсутствует последствие, то для его полного описания достаточно знать систему функций

Найдем выражение для 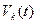. Нам понадобится следующая лемма.

Лемма. Для любого стационарного потока без последействия

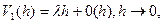(1)

где - некоторое постоянное число, называемое параметром потока, .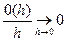

Рассмотрим простейший поток и определим вид функций

Пусть в некоторую обслуживающую систему поступают заявки на обслуживание. Система начинает функционировать, начиная с некоторого момента 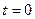. Рассмотрим отрезок времени (0,t+h] и определим, какова вероятность того, что за это время поступает, точно к требований. Точно к требований может поступить одним из к+1 различных несовместных способов, представленных в следующей схеме:

Промежутки времени	Количество требований, поступивших за данный промежуток времени
(0, t]	k	k-1	k-2	k-3	…
(t, t+h]					…	k-2	k-1	k

Воспользуемся теоремой сложения вероятностей для попарно несовместных событий:

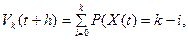
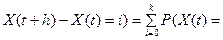
. Так как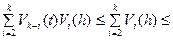

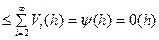в силу ординарности, то

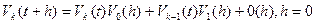. (2)

Найдем выражение для 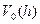. Учитывая, что

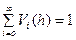, а также условие ординарности и формулу (1), получим

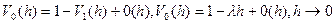(3)

Подставим выражения (1) и (3) в (2):

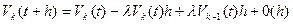, отсюда

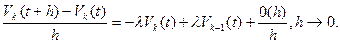
Так как существует предел правой части, то существует предел левой части и, переходя к пределу при 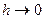, получаем

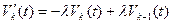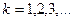, (4)

Таким образом, для определения 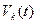получена бесконечная рекуррентная система линейных однородных дифференциальных уравнений (4).

Составим еще одно уравнение для определения 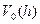. Это уравнение можно получить из условия .

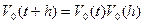Подставляя сюда (3), получаем 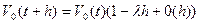. Тогда

.

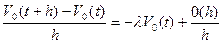Переходя к пределу при 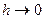: 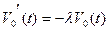. Проинтегрировав последнее уравнение, получим 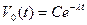. Для определения постоянной С воспользуемся равенством (3), из которого следует, что 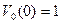. Таким образом 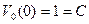и .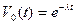

Вернемся к (4). Сделаем подстановку 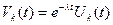, , 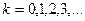где 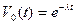и, значит 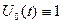. Вместо функции 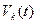, 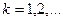будем искать функции 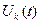, 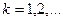Для функции 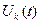получаем следующую систему уравнений:

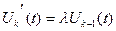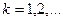, (5)

Начальные условия задаются равенствами:
, .

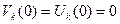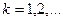Эти равенства получены из условий (1) и (3), в силу которых ,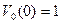

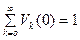и из условия . Подставив 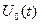в (5), получим .

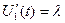Отсюда, учитывая начальные условия, имеем .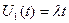

Далее, 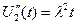и, учитывая начальные условия, .

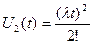По индукции находим 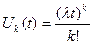, 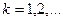и, значит,

,

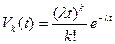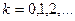
Таким образом, для простейшего потока число требований в промежутке времени длиной t распределено по закону Пуассона с параметром .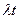

Мы доказали следующую теорему:

Теорема 2. Простейший поток описывается процессом Пуассона.

Рассмотрим физический смысл параметра . Легко показать, что для простейшего потока параметр равен среднему числу требований, поступивших в систему за единицу времени.

Действительно,

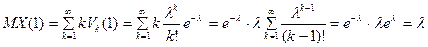
Дата добавления: 2014-01-07