Время обслуживания

Изучение и описание времени обслуживания является второй задачей после изучения и описания входящего потока. Время обслуживания является характеристикой функционирования каждого отдельного аппарата обслуживающей системы. Оно показывает, сколько времени затрачивается на обслуживание одного требования данным обслуживающим аппаратом.

Время обслуживания может быть константой или случайной величиной. Случай, когда время обслуживания является константой, не является типичным для систем массового обслуживания.

Если обозначить время обслуживания через 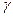, то его полной характеристикой будет закон распределения

.

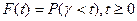Ясно, что F(t)=0 при t<0.

В теоретических исследованиях и во многих практических расчетах большое значение имеет показательный закон распределения времени обслуживания, при котором функция распределения времени обслуживания имеет вид:

а плотность распределения

Параметр 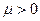, входящий в показательный закон распределения, имеет простой физический смысл. Величина обратная 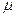, то есть является средним временем обслуживания.

Рис.3.

График функции распределения показательного закона имеет вид, представленный на Рис.3.

Теорема 3. При показательном законе распределения времени обслуживания закон распределения оставшегося времени обслуживания не зависит от того, сколько времени обслуживание уже длилось, и поэтому он такой же, как закон распределения полного времени обслуживания, то есть является показательным законом с тем же самым параметром .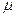

Доказательство. Для показательного закона распределения времени обслуживания для всех t, a>0 справедливо , поэтому

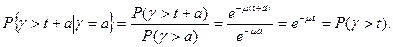
Дата добавления: 2014-01-07