Лекция 1. 3

Замкнутые механические системы. Закон сохранения импульса. Тела, образующие механическую систему, могут взаимодействовать как между собой, так и с телами, не входящими в данную систему. В соответствии с этим силы, действующие на тела системы, разделяют на внутренние и внешние. Внутренние силы обусловлены взаимодействием тел внутри системы. Внешние силы обусловлены воздействием на тела системы со стороны тел в эту систему не входящих. Если равнодействующая внешних сил, действующих на систему, равна нулю, или такие силы отсутствуют, то механическая система называется замкнутой. Рассмотрим механическую систему, состоящую из N взаимодействующих частиц (материальных точек). Обозначим силу, действующую на частицу с номером i со стороны частицы с номером j через Предположим, что кроме внутренних сил на каждую частицу действуют также внешние силы, равнодействующую которых для частицы обозначим через Запишем уравнение движения для всех N материальных точек, получим

Просуммируем левые и правые части полученной системы. Будем иметь:

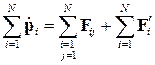. (4)

Заметим, что согласно третьему закону Ньютона

,

поэтому . Таким образом,

. (5)

Для замкнутой системы , поэтому для таких систем выполняется закон сохранения импульса:

,

или

, (6)

где – импульс механической системы. На основе соотношения (6) закон сохранения импульса формулируется следующим образом: импульс замкнутой механической системы остается постоянным. В случае, если сумма внешних сил не равна нулю, т.е. в случае незамкнутой механической системы,

, (7)

где - главный вектор (равнодействующая) внешних сил, приложенных к механической системе. Соотношение (7) выражает закон изменения импульса механической системы: изменение во времени импульса механической системы равно равнодействующей внешних сил, действующих на систему.

Центр масс механической системы. Уравнение движения центра масс. Система центра масс. Центром масс (или центром инерции) системы называется точка С, положение которой задается радиус-вектором, определяемым следующим образом

, (8)

где - масса и радиус-вектор i -й частицы, m – масса системы. продифференцируем соотношение (8) по времени, получим

.

Так как 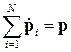, то

, (9)

т.е. импульс механической системы равен произведению массы системы на скорость движения ее центра масс.

Подставим теперь полученное соотношение (9) в (7), получим

. (10)

Соотношение (10) представляет собой уравнение движения центра масс механической системы.

Замечание: из (8) следует, что декартовы координаты центра масс определяются соотношениями

. (11)

Замечание: поскольку в замкнутой системе

,

то центр масс такой системы либо покоится, либо двигается равномерно и прямолинейно.

Система отсчета, в которой центр масс покоится, называется системой центра масс. Система центра масс является инерциальной.

Кинетическая энергия частицы. Рассмотрим уравнение движения материальной точки

.

В этом уравнении F есть результирующая внешних сил, действующих на материальную точку. Умножим обе части на перемещение частицы , получим

.

Перепишем последнее соотношение в виде

. (12)

Определение: кинетической энергией частицы называется скалярная величина T, определяемая соотношением

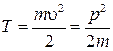. (13)

Из (12) следует, что в замкнутой системе () кинетическая энергия есть величина постоянная.

Если система не замкнута, то, как следует из (12),

, (14)

где - элементарная работа по перемещению точки, совершаемая силой F на пути . Возьмем интеграл от обеих частей (14) на пути частицы из точки 1 в точку 2, получим

,

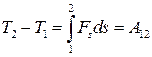. (15)

В (15) - значения кинетической энергии частицы в точках 1 и 2 соответственно, - работа силы на участке 1-2 траектории движения точки. Соотношение (15) означает, что работа результирующей всех сил, действующих на частицу, идет на приращение ее кинетической энергии.

Потенциальные (консервативные) силы. Потенциальная энергия. Силовое поле. Сила F, действующая на материальную точку называется потенциальной, если работа этой силы зависит только от начального и конечного положения материальной точки. Работа потенциальной силы по перемещению материальной точки на замкнутом участке траектории равна нулю, т.е.

. (16)

Действительно, если рассмотреть замкнутый контур Г (см. рис. 4), то из независимости работы от вида траектории следует, что работы и должны быть равны по модулю. В тоже время из рис. 4 ясно, что произведения на участках 1-2 и 2-1 будут иметь разные знаки. Поэтому

.

Рассмотрим теперь систему N материальных точек. Предположим, что на каждую точку системы действуют только потенциальные силы. Тогда суммарная работа, совершаемая этими силами, по изменению взаимного положения точек системы, т.е. изменение ее конфигурации, будет зависеть только от начального и конечного состояний этой системы. Зададим текущее состояние системы некоторой функцией U. Тогда работа по переводу системы из состояния 1 в состояние 2 будет равна

. (17)

Функцию U, определяющую текущее состояние системы, называют потенциальной энергией системы материальных точек.

Элементарная работа потенциальных сил может быть представлена в виде

. (18)

Из данного ранее определения потенциальной энергии вытекает, что

, (19)

где - равнодействующая потенциальных сил, действующих на i -ю материальную точку, - перемещение точки под действием этих сил.

Пусть теперь на каждую частицу рассматриваемой нами системы действуют внутренние и внешние потенциальные силы, а также внешние не потенциальные силы. В таком случае уравнение движения каждой точки системы следует представлять в виде

, (20)

где - равнодействующие внутренних потенциальных, внешних потенциальных и внешних не потенциальных сил соответственно. Под действием этих сил за время 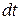i -я частица переходит из одной точки пространства в другую, перемещаясь на величину . Умножим левую и правую части (20) на это перемещение, при этом учтем, что . Получим

. (21)

С учетом (13) и (19) последнее соотношение может быть записано в виде

.

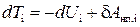Просуммировав последнее соотношение по всем N материальным точкам, находим

,

или

. (22)

Величина

, (23)

равная сумме кинетической и потенциальной энергий системы, называется полной механической энергией системы.

Интегрируя соотношение (23) при переходе системы из состояния 1 в состояние 2, находим

. (24)

Таким образом,

. (25)

Соотношения (24), (25) выражают собой закон изменения полной механической энергии системы, согласно которому изменение полной механической энергии системы равно работе внешних не потенциальных сил, действующих на систему. В качестве таких сил могут выступать, например, силы трения. Работа силы трения зависит от величины пройденного телом пути, т.е. от вида траектории его движения. Согласно определению элементарная работа равна

,

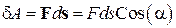где α – угол между векторами F и d s. Поскольку направление вектора силы трения всегда противоположно направлению вектора перемещения, работ сил трения всегда отрицательна. Последнее в соответствии с (25) означает, что движение частиц механической системы при наличии сил трения будет сопровождаться убылью полной механической энергии, так как

.

Конечно такое утверждение справедливо, если система не получает дополнительную энергию из каких-либо внешних источников. Пример (колебания маятника в воздухе).

Процесс убыли механической энергии системы, приводящий в частности к рассеянию ее в окружающее пространство, называется диссипацией. Силы, вызывающие такое рассеяние называют диссипативными.

В случае, если внешние не потенциальные силы отсутствуют, и (25) принимает вид

. (26)

Последнее соотношение есть математическая форма записи закона сохранения механической энергии: в отсутствии внешних не потенциальных сил полная механическая энергия системы остается постоянной.

Связь между потенциальной энергией и силой. Рассмотрим частицу, движущуюся под действием результирующей внешней потенциальной силы F. Согласно (18)

. (28)

С другой стороны

. (29)

Сопоставляя (28) и (29) находим, что

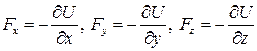. (30)

Анализируя (28) – (30) видим, что

. (31)

Оператор

называется оператором градиента. Заметим, что (31) определяет условие потенциальности (консервативности) силы, т.е. если сила потенциальная, то она с необходимостью должна удовлетворять условию (31).

Силовое поле. Если частица, будучи помещенной в любую точку рассматриваемой области пространства, оказывается под воздействием силы, то говорят, что в рассматриваемой области пространства существует силовое поле. Одним из примеров силового поля является поле сил земного тяготения. Другой пример силового поля, электростатическое поле, которое может быть создано, например, точечным зарядом. Как поле сил земного тяготения, так и поле точечного заряда характеризуются тем, что сила действующая на частицу, помещенную в такое поле, направлена по прямой, соединяющей частицу и некоторую неподвижную точку пространства (место расположения точечного заряда или центр Земли). При этом величина силы оказывается зависящей только от расстояния между этой точкой пространства и частицей, т.е. . Силовое поле, удовлетворяющее этим условиям, называется центральным. Если во всех точках поля силы, действующие на частицу одинаковы по величине, т.е. , то такое поле называется однородным. Если силовое поле не изменяется со временем, то поле называется стационарным, и не стационарным в противном случае.

Гравитационное поле. Напряженность и потенциал гравитационного поля. Ранее мы установили, что между любыми двумя частицами с массами m ₁ и m ₂ существует сила взаимодействия – сила гравитационного притяжения, равная по модулю

.

Так как данная сила с той или иной интенсивностью будет действовать на тела в не зависимости от их взаимного положения в пространстве, то можно говорить о том, что каждое тело, обладающее массой, создает вокруг себя силовое поле, называемое гравитационным. Наличие этого поля как раз и проявляется в том, что между двумя телами, помещенными на некотором расстоянии друг от друга, возникает сила гравитационного взаимодействия. Говорят еще, что тела взаимодействуют друг с другом посредством силового поля.

Рассмотрим тело массой m, помещенное в некоторую точку пространства. Сила взаимодействия этого тела с другим телом массой m ', помещенным на расстоянии r от него будет равна

. (32)

Как видно из (32), в независимости от массы второго тела отношение

есть величина, зависящая только от массы первого тела и от расстояния между телами. Последнее соотношение можно записать в виде

, (33)

где - напряженность гравитационного поля, - единичный вектор, направленный по радиус-вектору 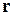. С учетом (33) соотношение (32) принимает вид

. (34)

Применительно к рассмотрению гравитационного поля Земли вблизи ее поверхности получаем

. (35)

Таким образом, известное нам ускорение свободного падения оказывается ни чем иным как напряженностью гравитационного поля Земли вблизи ее поверхности. Отметим также, что согласно (30)

,

откуда

. (36)

И вновь, аналогично показанному ранее, отношение

оказывается зависящим только от массы тела и расстояния между взаимодействующими телами, иначе расстояния до точки наблюдения. Эту величину обозначают

(37)

и называют потенциалом гравитационного поля. Заметим, что согласно (37) работа по перемещению частицы в таком поле из положения 1 в положение 2 равна

, (38)

т.е. работа равна произведению массы частицы на разность потенциалов гравитационного поля. Заметим также, что поскольку

,

а также

,

то

.

Последнее соотношение выражает связь между напряженностью гравитационного поля и его потенциалом.

Движение тела переменной массы. Реактивное движение. Формула Циолковского. Рассмотрим движение ракеты массой m, летящей по прямой. Пусть скорость выброса газов относительно ракеты равна u. Запишем уравнение движения нашей ракеты, учтя, что масса ракеты уменьшается вследствие выброса газов. Будем иметь

.

Рассмотрим рис. 5. Пусть ракета, имея в начальный момент массу m и двигаясь со скоростью , за время 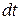выбросила назад порцию газов массой со скоростью u относительно себя. Порция газов массой , летящая назад со скоростью относительно неподвижной системы отсчета, будет иметь импульс .

После выброса газов скорость и масса ракеты изменятся, так что импульс ракеты станет равным . В начальный момент импульс системы был равен . После выброса газов - .

Изменение импульса системы

.

Последнее соотношение можно записать в виде

.

Здесь мы пренебрегли величиной , имеющей второй порядок малости, по отношению к другим слагаемым. Учтем теперь, что согласно правилу сложения скоростей Галилея

.

. (39)

Подставив (39) в уравнение движения найдем, что

,

или

, (40)

где

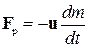
есть реактивная сила. Соотношение (40) впервые было получено И.В. Мещерским.

Предположим, что на ракету не действуют внешние силы. Тогда из (40) следует

. (41)

Запишем (41) в проекции на направление движения ракеты, при этом учтем, что , получим

,

или

.

Проинтегрируем это соотношение слева по , а справа по , получим

.

Соотношение

(42)

было получено К.Э. Циолковским и носит название формулы Циолковского.

Дата добавления: 2014-01-07