Эрмитов кубический интерполянт

На каждом интервале 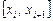функция 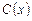является кубической и задаётся четырьмя коэффициентами . Для программы, основанной на таком представлении, потребуется массив для хранения 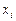и четыре массива и для коэффициентов кубической функции на каждом интервале. Это называется кусочно-кубическим представлением.

Используем другое, более наглядное представление.

Определим базисных функций и , 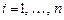. Пусть каждая из них является кусочно-кубической с непрерывной на 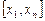производной. Тогда и любая их линейная комбинация обладает теми же свойствами. Определение этих функций должно гарантировать, что

.

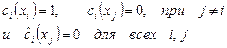В этом случае функция

является эрмитовым кубическим интерполянтом при любом выборе .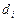

Потребуем ещё, чтобы

.

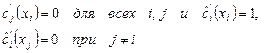Тогда

.

Все эрмитовы кубические интерполянты представляют собой кусочно-кубические функции, интерполирующие по заданным точкам и имеющие по одной непрерывной производной. Значения производных в узлах интерполяции задаются числами 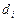. Такая форма представления особенно полезна, если, кроме самих значений в точках 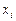, известны ещё и величины углов наклона касательных к интерполируемой функции. В этом случае в качестве 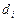естественно брать заданные угловые коэффициенты.

Эрмитов кубический интерполянт не является единственным. Существует 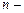параметрическое семейство кусочно-кубических функций, которые интерполируют 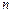данных значений и имеют по одной непрерывной производной.

Детали эрмитовой кубической интерполяции.

Пусть 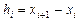. Определим на каждом из интервалов 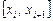, , 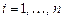четыре кубические функции

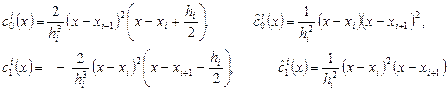
Теперь определим 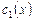и как

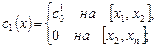
Положим для

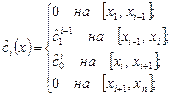
а для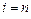

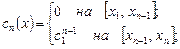
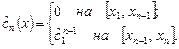
Наконец, определим

.

Обрисуем свойства этих функций на примере 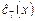. По данному выше определению 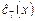тождественно равна нулю пр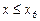и и .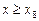

Для 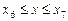имеем .

Для имеем .

Из этих формул видно, что функция 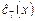определена при всех 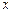и является кусочно-полиномиальной. Она обращается в нуль в каждом узле. В точках и 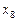у неё нули второго порядка, следовательно, в этих точках и производная обращается в нуль.

В узле 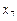производную можно вычислить по одной из двух формул, в зависимости от того, приближаемся мы к 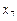слева или справа.

Производная слева равна

,

производная справа равна

.

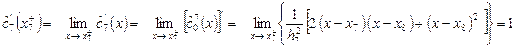Поскольку односторонние производные с обеих сторон равны, то .

Можно доказать, что функции и , 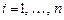непрерывны и имеют непрерывную производную на всем интервале 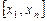, непрерывную производную имеет и сама функция 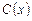, следовательно, она является эрмитовым кубическим интерполянтом. Функцию 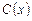легко вычислить, если известны величины 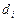. Для нахождения интерполянта в произвольной фиксированной точке 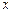достаточно заметить, что функции и отличны от нуля не более чем на двух интервалах. Поэтому большинство членов в сумме тождественно равны нулю; надо учитывать не более четырёх слагаемых.

Итак, вычисление значения 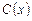включает в себя, во-первых, локализацию 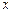в некотором интервале (между 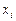и 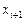), во-вторых, вычисление членов 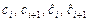, в-третьих, умножение на требуемые 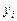и 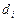и суммирование.

Дата добавления: 2014-01-07