Кубические сплайны

Сплайном называется функция, которая вместе с несколькими производными непрерывна на всем заданном отрезке 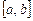или 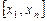, а на каждом локальном отрезке 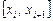в отдельности является некоторым алгебраическим многочленом.

Максимальная по всем частичным отрезкам степень полиномов называется степенью сплайна, а разность между степенью сплайна и порядком наивысшей непрерывной на 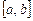производной – дефектом сплайна.

Например, непрерывная кусочно-линейная функция (ломаная) является сплайном первой степени с дефектом, равным единице, так непрерывна только сама функция (нулевая производная), а первая производная уже имеет разрыв.

На практике наиболее широкое распространение получили сплайны третьей степени, имеющие на 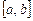непрерывную, по крайней мере, первую производную.

Величина 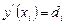называется наклоном сплайна в точке (узле) .

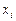Кубический сплайн, заданный локально, – это интерполирующая функция в виде полинома третьей степени, вычисляемая по формуле

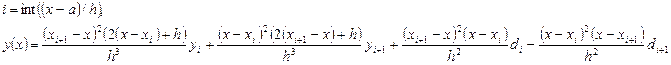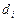где и 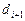- первые производные :

; .

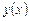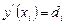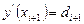Производные локального сплайна могут задаваться тремя способами.

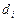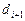Способ 1. Производные и вычисляются с помощью формул численного дифференцирования по трём точкам:

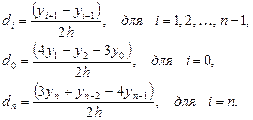
Способ удобен тем, что для задания сплайна требуется вводить лишь ординаты 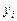(значения 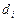вычисляются программой). Для уменьшения времени многократных вычислений 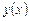желательно предварительно вычислить массив 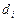и хранить его в памяти.

Способ 2. Значения 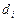(вычисленные отдельно или полученные из графиков как наклоны его в узлах) задаются непосредственно в виде массива .

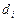Способы 1 и 2 называются локальными, поскольку с их помощью на каждом частичном отрезке 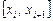сплайн строится отдельно (непосредственно по формуле). При этом тем не менее соблюдается непрерывность в узлах 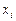производной 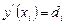. Непрерывность же второй производной 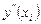в узлах не гарантируется. Поэтому дефект такого сплайна равен двум. Это эрмитовы кубические сплайны, рассмотренные ранее.

Способ 3. (глобальный способ). Другой подход у выбору 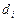заключается в том, чтобы заставить функцию 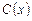удовлетворять дополнительным условиям. Разумно требовать, чтобы эта функция была более гладкой, т. е. чтобы отдельные составляющие её полиномы при стыковке в узлах давали непрерывную вторую производную. Найдём вторые производные слева и справа от узла 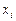на отрезке :

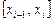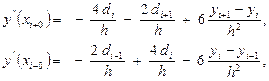
Потребуем непрерывность второй производной в узлах :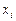

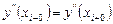при всех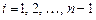

и приходим к следующей системе линейных алгебраических уравнений относительно наклонов:

, . (*)

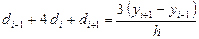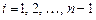Так как неизвестных 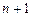, то нужно задавать ещё два условия, которые называют краевыми (они обычно связаны с «крайними» значениями ).

Дадим три варианта краевых условий.

1. Если известны , то задаём

.

1. Производные 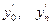аппроксимируем формулами численного дифференцирования третьего порядка с отбрасыванием остаточных членов:

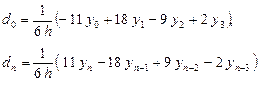
1. В некоторых случаях бывают известны вторые производные на концах отрезка 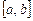, т. е. . Тогда приходим к краевым условиям

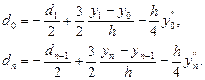
Краевые условия можно комбинировать, т. е. в левом и правом узлах выбирать их независимо.

Система (*) при всех рассмотренных краевых условиях имеет единственное решение, для нахождения которого могут быть применены методы прогонки итераций.

Решая систему (*) при выбранных краевых условиях, находим наклоны 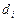во всех узлах. Затем задаём сплайн на каждом локальном отрезке. Построенный данным глобальным способом сплайн имеет дефект не больше единицы, так как этот сплайн обладает на отрезке 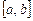непрерывной второй производной.

Дата добавления: 2014-01-07